摘要：21． 如图.M是抛物线上y2=x上的一点.动弦ME.MF分别交x轴于A.B两点.且MA=MB. (1)若M为定点.证明:直线EF的斜率为定值, (2)若M为动点.且∠EMF=90°.求△EMF的重心G的轨迹方程. [思路点拨]本题涉及抛物线与直线相交的有关知识. [正确解答](1)设M(y,y0).直线ME的斜率为k 则直线MF的斜率为-k. 消 所以直线EF的斜率为定值 (2) 同理可得 设重心G(x, y).则有 [解后反思]这是一道重要的数学问题,它属于解析几何范畴,几乎是高考数学每年的必考内容之一,此类问题一定要 大胆假设,细心求解 ,根据题目要求先将题目所涉及的未知量都可以设出来,然后根据题目把所有的条件都变成等式,一定可以求出来,当然求的过程中,采取适当的小技巧,例如化简或适当分类讨论,可以大为简化过程,而且会尽量多多得分,同时这一类题目也需要很强的计算能力.
网址：http://m.1010jiajiao.com/timu3_id_4469190[举报]
(本小题满分12分) 设椭圆C1：
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：
与y轴的交点为B，且经过F1，F2点．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0，
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值．
. (本小题满分12分）
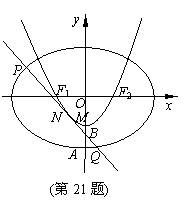
如图，设抛物线C1:
的准线与x轴交于F1，焦点为F2 ；以F1,F2为焦点，离心率
的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q，M是抛物线上一动点，且M在P与Q之间运动.
(I)当m = 1时，求椭圆C2的方程；
(II)当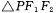
的边长恰好是三个连续的自然数时，求
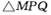面积的最大值.
查看习题详情和答案>>
. (本小题满分12分）
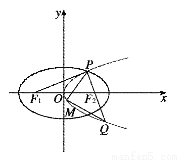
如图，设抛物线C1:
的准线与x轴交于F1，焦点为F2；以F1,F2为焦点，离心率
的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q，M是抛物线上一动点，且M在P与Q之间运动.
(I)当m =1时，求椭圆C2的方程；
(II)当
的边长恰好是三个连续的自然数时，求
面积的最大值.
如图，设抛物线C1:
的准线与x轴交于F1，焦点为F2；以F1,F2为焦点，离心率的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q，M是抛物线上一动点，且M在P与Q之间运动.(I)当m =1时，求椭圆C2的方程；
(II)当
的边长恰好是三个连续的自然数时，求面积的最大值.
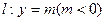上任意一点，过点M引抛物线E的两条切线分别交x轴于点S , T，切点分别为B、A。
上移动时，直线AB恒过焦点F，求
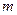的值。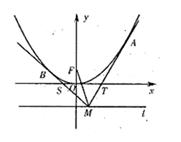
上任意一点，过点M引抛物线E的两条切线分别交x轴于点S , T，切点分别为B、A。
上移动时，直线AB恒过焦点F，求
的值。