摘要:15.如图.在三棱锥P-ABC中.PA=PB=PC=BC. 且.则PA与底面ABC所成角为 . [思路点拨]本题主要考查直线与平面所成的角的求法,关键是 确定点P在底面的射影O的位置. [正确解答]过P作.交底面于O.连结AO并延长交BC于D.连结PD.则PD.AD均垂直于BC.所以AB=AC.PA与底面ABC所成角为. 设AC=1.则PA=PB=PC=BC=... .所以. [解后反思]熟练掌握三角形的“四心 是快速解该题的关键.外心:三角形三条中垂线的交点,性质外心到三角顶点距离相等,内心:内角平分线的交点,性质是内心到三边距离相等,垂心:三条高线的交点,重心:三条中线的交点,另外记住一些结论也是大有裨益的,比如在三棱锥P-ABC中(1)若P到三个顶点的距离相等,则P在底面的射影是ABC的外心,(2)若P到三边的距离相等,则P在底面的射影是的内心,(3)若则且P在底面的射影是的垂心.
网址:http://m.1010jiajiao.com/timu3_id_4469184[举报]
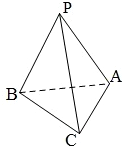 如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC=
如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC=
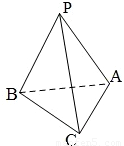 如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC=
如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC=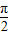 ,则PA与底面ABC所成角为 .
,则PA与底面ABC所成角为 . 如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC=
如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC= ,则PA与底面ABC所成角为 .
,则PA与底面ABC所成角为 . 如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC=
如图,在三棱锥P-ABC中,PA=PB=PC=BC,且∠BAC= ,则PA与底面ABC所成角为 .
,则PA与底面ABC所成角为 .