摘要:g(t)的最小值为0. 提示:讨论对称轴x=-1与区间端点t,t+1的关系. 8.[,18] 基础训练8答案一.1.C 2.D 3.B 二.4.
网址:http://m.1010jiajiao.com/timu3_id_4467929[举报]
已知二次函数f(x)=ax2+bx+c.
(1)若f(0)=1,b=-a-1,解关于x不等式f(x)<0;
(2)若f(x)的最小值为0,且a<b,设
=t,请把
表示成关于t的函数g(t),并求g(t)的最小值.
查看习题详情和答案>>
(1)若f(0)=1,b=-a-1,解关于x不等式f(x)<0;
(2)若f(x)的最小值为0,且a<b,设
| b |
| a |
| a+b+c |
| b-a |
设二次函数f(x)=ax2+bx+c(a≠0)满足条件:①当x∈R时,f(x-4)=f(2-x),且x≤f(x)≤
(1+x2);②f(x)在R上的最小值为0.
(1)求f(1)的值及f(x)的解析式;
(2)若g(x)=f(x)-k2x在[-1,1]上是单调函数,求k的取值范围;
(3)求最大值m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
查看习题详情和答案>>
| 1 | 2 |
(1)求f(1)的值及f(x)的解析式;
(2)若g(x)=f(x)-k2x在[-1,1]上是单调函数,求k的取值范围;
(3)求最大值m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
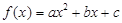 .
.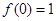 ,
,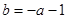 ,解关于x不等式
,解关于x不等式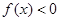 ;
;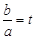 ,请把
,请把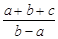 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.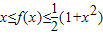 ;②f(x)在R上的最小值为0.
;②f(x)在R上的最小值为0.