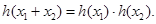摘要：16． 在中学数学中.从特殊到一般.从具体到抽象是常见的一种思维形式.如从指数函数中可抽象出的性质,从对数函数中可抽象出的性质.那么从函数 可抽象出的性质. 17．在平面几何中ΔABC的∠C内角平分线CE分AB所成线段的比 把这个结论类比到空间:在三棱锥A-BCD中DEC平分二面角A-CD-B且与AB相交于E.则得到类比的结论是 .
网址：http://m.1010jiajiao.com/timu3_id_4466173[举报]
14、在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维方式．如从指数函数中可抽象出f（x1+x2）=f（x1）•f（x2）的性质；从对数函数中可抽象出f（x1•x2）=f（x1）+f（x2）的性质，那么从函数
查看习题详情和答案>>
y=kx（k≠0）
．（写出一个具体函数即可）可抽象出f（x1+x2）=f（x1）+f（x2）的性质．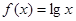
可抽象出
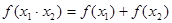的性质，那么由
= （填一个具体的函数）可抽象出性质
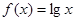可抽象出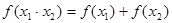
的性质，那么由
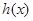= （填一个具体的函数）可抽象出性质