题目内容
14、在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维方式．如从指数函数中可抽象出f（x1+x2）=f（x1）•f（x2）的性质；从对数函数中可抽象出f（x1•x2）=f（x1）+f（x2）的性质，那么从函数
y=kx（k≠0）
．（写出一个具体函数即可）可抽象出f（x1+x2）=f（x1）+f（x2）的性质．分析：由f（x）=x，f（x1+x2）=x1+x2=f（x1）+f（x2），联想到正比例函数的性质可得答案．
解答：解：令y=f（x）=kx，k≠0，k为常数，
则f（x1+x2）=k（x1+x2）=kx1+kx2=f（x1）+f（x2），
故所求的函数可以是 y=kx．
则f（x1+x2）=k（x1+x2）=kx1+kx2=f（x1）+f（x2），
故所求的函数可以是 y=kx．
点评：本题考查抽象函数及其应用．
练习册系列答案
相关题目
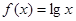可抽象出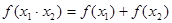
的性质，那么由
= （填一个具体的函数）可抽象出性质
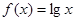可抽象出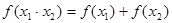
的性质，那么由
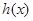= （填一个具体的函数）可抽象出性质