摘要：21．如图.在直角坐标系中.点A().设与x轴正方向的夹角分别为α.β.γ.若. (I)求点P的轨迹G的方程, 的直线与轨迹G交于不同两点M.N.问在x轴上是否存在一点.使△MNE为正三角形.若存在求出值,若不存在说明理由. 高考数学考前模拟训练(二)
网址：http://m.1010jiajiao.com/timu3_id_4464878[举报]
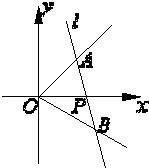如图，在直角坐标系中，射线OA：x-y=0（x≥0），OB：| 3 |
过点P（1，0）作直线分别交射线OA、OB于A、B点．
①当AB的中点为P时，求直线AB的方程；
②当AB的中点在直线y=
| 1 |
| 2 |
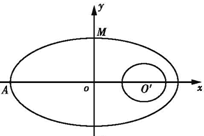如图，在直角坐标系中，中心在原点，焦点在x轴上的椭圆G的离心率为
| ||
| 4 |
| 4 |
| 9 |
（Ⅰ）求椭圆G的方程；
（Ⅱ）过M（0，1）作圆O′的两条切线交椭圆于E、F，判断直线EF与圆的位置关系，并证明．
如图，在直角坐标系
中，已知椭圆
的离心率e＝
，左右两个焦分别为
．过右焦点
且与
轴垂直的
直线与椭圆
相交M、N两点，且|MN|=1．
(Ⅰ) 求椭圆的方程；
(Ⅱ) 设椭圆的左顶点为A,下顶点为B，动点P满足
，
（
）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆上. 
中，已知椭圆
的离心率e＝
，左右两个焦分别为
．过右焦点
且与
轴垂直的
相交M、N两点，且|MN|=1．
，
）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆
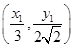的轨迹C2的方程．