摘要:13.已知抛物线的焦点在直线上.若抛物线作如下移动.其 焦点沿直线滑动.对称轴作平行移动.那么当焦点移动到时.抛物线的 方程是 .
网址:http://m.1010jiajiao.com/timu3_id_4464806[举报]
已知抛物线![]() 的焦点F以及椭圆
的焦点F以及椭圆![]() (
(![]()
![]() )的上、下焦点及左、右顶点均在圆O:
)的上、下焦点及左、右顶点均在圆O:![]() 上。
上。
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(2)过点F的直线交抛物线![]() 于A,B两不同点,交y轴于点N,已知
于A,B两不同点,交y轴于点N,已知![]() ,则
,则![]() 是否为定值?若是,求出其值;若不是,说明理由。
是否为定值?若是,求出其值;若不是,说明理由。
已知抛物线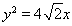 的焦点为椭圆
的焦点为椭圆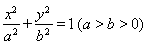 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: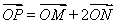 ,直线
,直线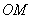 与
与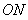 的斜率之积为
的斜率之积为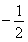 ,证明:存在定点
,证明:存在定点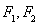 使
使
得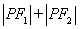 为定值,并求出
为定值,并求出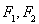 的坐标;
的坐标;
(3)若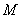 在第一象限,且点
在第一象限,且点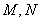 关于原点对称,
关于原点对称,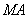 垂直于
垂直于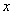 轴于点
轴于点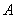 ,连接
,连接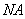 并延长交椭圆于点
并延长交椭圆于点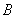 ,记直线
,记直线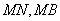 的斜率分别为
的斜率分别为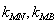 ,证明:
,证明: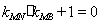 .
.
查看习题详情和答案>>
 的焦点
的焦点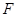 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆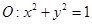 上.
上.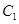 和椭圆
和椭圆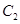 的标准方程;
的标准方程;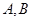 两不同点,交
两不同点,交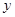 轴于点
轴于点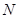 ,已知
,已知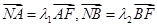 ,求
,求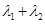 的值;
的值;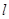 交椭圆
交椭圆 两不同点,
两不同点,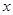 轴的射影分别为
轴的射影分别为 ,
, ,若点
,若点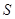 满足
满足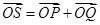 ,证明:点
,证明:点 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程; 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则