摘要：20．设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3, 且数列{an+1-an }是等差数列.数列{bn-2}是等比数列. (Ⅰ)求数列{an}和{bn}的通项公式, (Ⅱ)是否存在k∈N*.使ak-bk∈(0.)?若存在.求出k,若不存在.说明理由. 解:(I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1 ∴an+1-an=(a2-a1)+(n-1)·1=n-3 n≥2时.an=( an-an-1)+( an-1-an-2)+-+( a3-a2)+( a2-a1)+ a1 =+(-2)+6 = n=1也合适. ∴an= --------3分 又b1-2=4.b2-2=2 .而 ∴bn-2=(b1-2)·()n-1即bn=2+8·()n-6分 ∴数列{an}.{bn}的通项公式为:an= .bn=2+()n-3 (II)设 当k≥4时为k的增函数.-8·()k也为k的增函数.而f(4)= ∴当k≥4时ak-bk≥------10分 又f=0 ∴不存在k. 使f(k)∈(0.)----12分
网址：http://m.1010jiajiao.com/timu3_id_4463227[举报]
设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}(n∈N*)是等差数列，数列{bn-2}(n∈N*)是等比数列.
(1)求数列{an}和{bn}的通项公式；
(2)是否存在k∈N*,使ak-bk∈(0,
)?若存在，求出k；若不存在，说明理由.
设数列{an}和{bn}满足:a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列.
(1)求列数{an}和{bn}的通项公式.
(2)是否存在k∈N*,使ak-bk∈(0,
)?若存在,求出k;若不存在,请说明理由.
设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}{n∈N*}是等差数列，数列{bn-2}{n∈N*}是等比数列.
（1）求数列{an}和{bn}的通项公式；
（2）是否存在k∈N*,使ak-bk∈(0,
)?若存在，求出k，若不存在，说明理由.
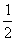）？若存在，求出k；若不存在，说明理由。