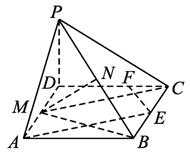
摘要：已知ABCD是矩形.PD⊥平面ABCD.PD=DC=a..M.N分别是AD.PB的中点. (Ⅰ)求证:平面MNC⊥平面PBC, (Ⅱ)求点A到平面MNC的距离. 解:(I)连PM.MB ∵PD⊥平面ABCD ∴PD⊥MD-1分 ∴PM=BM 又PN=NB ∴MN⊥PB---3分 得NC⊥PB∴PB⊥平面MNC--5分 平面PBC ∴平面MNC⊥平面PBC--6分 (II)取BC中点E.连AE.则AE//MC∴AE//平面MNC. A点与E点到平面MNC的距离相等-7分 取NC中点F.连EF.则EF平行且等于BN ∵BN⊥平面MNC ∴EF⊥平面MNC.EF长为E 点到平面MNC的距离--9分 ∵PD⊥平面ABCD. BC⊥DC ∴BC⊥PC. 即点A到平面MNC的距离为--12分

网址：http://m.1010jiajiao.com/timu3_id_4463226[举报]