摘要: 解:(I)设的公差为d.的公比为.由已知得方程组: 化简后.得 ---------------2分 将并化简后.得 解得或(舍) 将代入分别求出-----------5分 则-----------------7分 (II)--------------------8分 考查不等式.当时不成立.时成立.猜想取 ---------------------------------10分 用数学归纳法证明如下: (1)当时..不等式成立. (2)假设时.不等式成立.即. 则当时..不等式也成立. 综合.对任意的自然数n.不等式成立.--12分 评分标准说明:列方程组正确2分.解方程组每个解正确各1分.通项公式写对各1分.代入计算正确占1分.猜想占2分.用数学归纳法证明占4分.
网址:http://m.1010jiajiao.com/timu3_id_4460933[举报]
设数列{an}是公差为d的等差数列,其前n项和为Sn.
(1)已知a1=1,d=2,
(i)求当n∈N*时,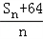 的最小值;
的最小值;
(ii)当n∈N*时,求证: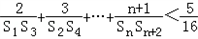 ;
;
(2)是否存在实数a1,使得对任意正整数n,关于m的不等式am≥n的最小正整数解为3n﹣2?若存在,则求a1的取值范围;若不存在,则说明理由.
查看习题详情和答案>>
(1)已知a1=1,d=2,
(i)求当n∈N*时,
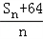 的最小值;
的最小值;(ii)当n∈N*时,求证:
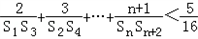 ;
;(2)是否存在实数a1,使得对任意正整数n,关于m的不等式am≥n的最小正整数解为3n﹣2?若存在,则求a1的取值范围;若不存在,则说明理由.
| |||||||||||||||