摘要：有的应用题中的数列递推关系.an与an-1的差不是一个常数.但是所得的差f(n)本身构成一个等差或等比数列.这在一定程度上增加了递推的难度. 例2.某产品具有一定的时效性.在这个时效期内.由市场调查可知.在不作广告宣传且每件获利a元的前提下.可卖出b件.若作广告宣传.广告费为n千元时比广告费为(n-1)千元时多卖出件.(n∈N*). (1)试写出销售量s与n的函数关系式, (2)当a=10,b=4000时厂家应生产多少件这种产品.做几千元广告.才能获利最大? 分析:对于(1)中的函数关系.设广告费为n千元时的销量为sn,则sn-1表示广告费为(n-1)元时的销量.由题意.sn--sn-1=.可知数列{sn}不成等差也不成等比数列.但是两者的差构成等比数列.对于这类问题一般有以下两种方法求解: 解法一.直接列式:由题.s=b++++-+=b(2-) (广告费为1千元时.s=b+,2千元时.s=b++,-n千元时s=b++++-+) 解法二.设s0表示广告费为0千元时的销售量. 由题:.相加得Sn-S0=+++-+, 即s=b++++-+=b(2-). (2)b=4000时.s=4000(2-),设获利为t,则有t=s·10-1000n=40000(2-)-1000n 欲使Tn最大.则:.得.故n=5,此时s=7875. 即该厂家应生产7875件产品.做5千元的广告.能使获利最大.
网址：http://m.1010jiajiao.com/timu3_id_4460691[举报]
设数列{an}的前n项和为Sn，若对于任意的n∈N*,都有Sn=2an-3n,
(1)求数列{an}的首项与递推关系式an+1=f(an);
(2)先阅读下面定理，若数列{an}有递推关系an+1=Aan+B,其中A、B为常数，且A≠1,B≠0,则数列{an-
}是以A为公比的等比数列，请你在第（1）题的基础上应用本定理，求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn.
查看习题详情和答案>>设数列{an}的前n项和Sn，若对于任意的n∈N*，都有Sn＝2an－3n．
(1)求数列{an}的首项与递推关系式an+1＝f(an)；
(2)先阅读下面的定理，若数列有递推关系：an+1＝Aan＋B，其中A、B为常数，且A≠1，B≠0，则数列{an－
}是以A为公比的等比数列，请你在第(1)题的基础上应用本定理，求数列{an}的通项公式；
(3)求数列{an}的前n项和Sn．
设数列{an}的前n项和为Sn，若对于任意的n∈N*，都有Sn=2an-3n．
（1）求数列{an}的首项a1与递推关系式：an+1=f（an）；
（2）先阅读下面定理：“若数列{an}有递推关系an+1=Aan+B，其中A、B为常数，且A≠1，B≠0，则数列{an-
}是以A为公比的等比数列．”请你在第（1）题的基础上应用本定理，求数列{an}的通项公式；
（3）求数列{an}的前n项和Sn． 查看习题详情和答案>>
（1）求数列{an}的首项a1与递推关系式：an+1=f（an）；
（2）先阅读下面定理：“若数列{an}有递推关系an+1=Aan+B，其中A、B为常数，且A≠1，B≠0，则数列{an-
| B | 1-A |
（3）求数列{an}的前n项和Sn． 查看习题详情和答案>>
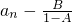是以A为公比的等比数列．”请你在第（1）题的基础上应用本定理，求数列{an}的通项公式；