摘要：21． 已知函数: (Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立. (Ⅱ)当f(x)的定义域为[a+,a+1]时.求证:f(x)的值域为[-3.-2], (Ⅲ)设函数g(x)=x2+|(x-a)f(x)| , 当求g(x) 的最小值 . 已知二次函数(R.0)． (I)当0＜＜时.(R)的最大值为.求的最小值． (II)如果[0.1]时.总有||．试求的取值范围． (III)令.当时.的所有整数值的个数为.求证数列的前项的和 长沙市实验中学2008届高三第一学期
网址：http://m.1010jiajiao.com/timu3_id_4457475[举报]
.(本小题满分14分)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120～130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. 
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
.(本小题满分14分)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120～130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
查看习题详情和答案>>
(本小题满分14分) 某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120～130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于
|
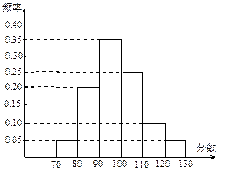
的离心率
，直线
过
、
两点，原点
到
.
作直线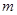
交双曲线于
两点，若
，求直线