摘要: 设数列的前项和为.对一切.点都在函数的图像上. (Ⅰ)求数列的通项公式, (Ⅱ)将数列依次按1项.2项.3项.4项循环地分为 分别计算各个括号内各数之和.设由这些和按原来括号的前后顺序构成的数列.求 (Ⅲ)设为数列的前项积.是否存在实数.使得不等式对一切都成立?若存在.求出的取值范围,若不存在.请说明理由. 解:猜想.数学归纳法证明,----------------------------4分 (II)因为.所以数列依次按1项.2项.3项.4项循环地分为....-.每一次循环记为一组.由于每一个循环含有4个括号,故是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列.且公差为20.同理.由各组第4个括号中所有第2个数.所有第3个数.所有第4个数分别组成的数列也都是等差数列.且公差均为20.故各组第4个括号中各数之和构成等差数列.且公差为80.注意到第一组中第4个括号内各数之和是68.所以=68+24+80=1988.又=22.所以=2010.-------------8分 因为.故. 所以. 又. 故对一切都成立.就是 对一切都成立.--------------10分 设.则只需即可. 由于. 所以.故是单调递减.于是. 令.即. 解得.或. 综上所诉.使得所给不等式对一切都成立的实数存在.的取值范围是.-------------------------------------------------------12分 本资料由 提供!
网址:http://m.1010jiajiao.com/timu3_id_4454392[举报]
(本题满分12分)已知数列{an}的前n项和为Sn,点(n,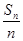 )在直线y=
)在直线y=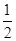 x+
x+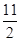 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=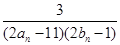 ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn>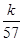 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
查看习题详情和答案>>
 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 都在函数
都在函数 的图像上.
的图像上. 的通项公式;
的通项公式; ,求数列
,求数列 的通项公式.
的通项公式. 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 。
。 的值;
的值; 的前
的前 ,且
,且 ,证明:对一切正整数
,证明:对一切正整数
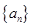 的前
的前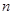 项和为
项和为 ,满足
,满足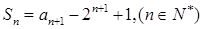 ,且
,且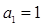 。
。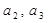 的值;
的值;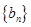 的前
的前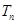 ,且
,且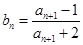 ,证明:对一切正整数
,证明:对一切正整数