摘要:平面M.N不重合.在M内取4个点.在N内取5个点.这些点最多能确定的平面有 个翰林汇
网址:http://m.1010jiajiao.com/timu3_id_4453625[举报]
(2012•邯郸一模)在平面直角坐标系中,点P(x,y)为动点,已知点A(
,0),B(-
,0),直线PA与PB的斜率之积为-
.
(I)求动点P轨迹E的方程;
( II)过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过定点.
查看习题详情和答案>>
| 2 |
| 2 |
| 1 |
| 2 |
(I)求动点P轨迹E的方程;
( II)过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过定点.
设α、β、γ是三个不重合的平面,m、n是不重合的直线,给出下列命题:
①若α⊥β,β⊥γ,则α⊥γ;②若m∥α,n∥β,α⊥β,则m⊥n;③若α∥β,γ∥β,则α∥γ;④若m、n在γ内的射影互相垂直,则m⊥n.
其中错误命题的个数为
A.0 B.1 C.2 D.3
查看习题详情和答案>>
在平面直角坐标系中,点P(x,y)为动点,已知点 ,
, ,直线PA与PB的斜率之积为
,直线PA与PB的斜率之积为 .
.
(I)求动点P轨迹E的方程;
( II)过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过定点.
查看习题详情和答案>>
 ,
, ,直线PA与PB的斜率之积为
,直线PA与PB的斜率之积为 .
.(I)求动点P轨迹E的方程;
( II)过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过定点.
查看习题详情和答案>>
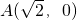 ,
,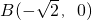 ,直线PA与PB的斜率之积为
,直线PA与PB的斜率之积为 .
.