假设太阳系中天体的密度不变,天体直径和天体之间距离都缩小到原来的一半,地球绕太阳公转近似为匀速圆周运动,则下列物理量变化正确的是( )
| A.地球的向心力变为缩小前的一半 |
B.地球的向心力变为缩小前的 |
| C.地球绕太阳公转周期与缩小前的相同 |
| D.地球绕太阳公转周期变为缩小前的一半 |
下表是火星和地球部分数据对照表,把火星和地球视为匀质理想球体,它们绕太阳的运动近似看作匀速圆周运动,从表中数据可以分析得出不正确的是( )
| | 质量 (kg) | 公转周期 (d天) | 自转周期 (h小时) | 近似公转轨道半径(m) | 星球半径 (m) |
| 火星 | 6.421×1023 | 686.98 | 24.62 | 2.28×1011 | 3.395×106 |
| 地球 | 5.976×1024 | 365.26 | 23.93 | 1.50×1011 | 6.378×106 |
B.地球公转动能较大
C.火星的第一宇宙速度较大
D.火星两极处地表重力加速度较小
地球赤道地面上有一物体随地球的自转而做圆周运动,所受的向心力为F1,向心加速度为a1,线速度为v1,角速度为ω1;绕地球表面附近做圆周运动的人造卫星(高度忽略)所受的向心力为F2 ,向心加速度为a2,线速度为v2,角速度为ω2;地球同步卫星所受的向心力为F3 ,向心加速度为a3,线速度为v3 ,角速度为ω3;地球表面重力加速度为g ,第一宇宙速度为v ,假设三者质量相等,则下列结论正确的是 ( )
| A.F1=F2>F3 | B.a1=a2=g>a3 |
| C.v1=v2=v>v3 | D.ω1=ω3<ω2 |
美国宇航局在2011年12月5日宣布,他们在太阳系外发现了一颗类似地球的、可适合人类居住的行星——“开普勒-22b”,该行星环绕一颗恒星运动的周期为290天,它距离地球约600光年,体积是地球的2.4倍.已知万有引力常量和地球表面的重力加速度,假定该行星环绕这颗恒星运动的轨迹为圆轨道,根据以上信息,下列推理中正确的是( )
| A.若已知该行星的轨道半径,可求出该行星所受的万有引力 |
| B.根据地球的公转周期与轨道半径,可求出该行星的轨道半径 |
| C.若该行星的密度与地球的密度相等,可求出该行星表面的重力加速度 |
| D.若已知该行星的轨道半径,可求出恒星的质量 |
目前在地球同步轨道上运行的同步卫星,下列说法中正确的是( )
| A.向心力大小相同 | B.周期相同 |
| C.向心加速度相同 | D.离地心的距离相同 |
“嫦娥一号”卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测。已知卫星绕月运动的周期约为127分钟,月球绕地球运动的轨道半径与卫星绕月球运动的轨道半径之比约为220。利用上述数据以及日常的天文知识,可估算出地球对卫星与月球对卫星的万有引力的比值约为( )
| A.2×10-3 | B.0.2 | C.7 | D.2×102 |
某研究小组用天文望远镜对一颗行星进行观测,发现该行星有一颗卫星,卫星在行星的表面附近绕行,并测得其周期为T,已知引力常量为G,根据这些数据可以估算出( )
| A.行星的质量 | B.行星的半径 |
| C.行星的平均密度 | D.行星表面的重力加速度 |
太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球公转速度的7倍,轨道半径约为地球公转道半径的2×109倍,为了粗略估算银河系中恒星的数目,可认为银河系中所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳质量,则银河系中恒星数目约为( )
| A.109 | B.1011 | C.1013 | D.1015 |
一行星绕恒星作圆周运动。由天文观测可得,其运动周期为T,速度为v,引力常量为G,则
A.恒星的质量为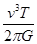 | B.行星的质量为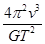 |
C.行星运动的轨道半径为 | D.行星运动的加速度为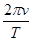 |



