如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度大小为 ,这物体在斜面上上升的最大高度为h,则在这一过程中( )
,这物体在斜面上上升的最大高度为h,则在这一过程中( ) 
A.重力势能增加了 |
B.机械能损失了 |
| C.动能损失了mgh |
D.合外力对物体做功为 |
如图所示,将一轻弹簧下端固定在倾角为θ的粗糙斜面底端,弹簧处于自然状态时上端位于A点。质量为m的物体从斜面上的B点由静止下滑,与弹簧发生相互作用后,最终停在斜面上。下列说法正确的是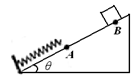
| A.物体最终将停在A点 |
| B.物体第一次反弹后不可能到达B点 |
| C.整个过程中重力势能的减少量大于克服摩擦力做的功 |
| D.整个过程中物体的最大动能小于弹簧的最大弹性势能 |
如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点。下列说法中正确的是( )
| A.小球从A出发到返回A的过程中,位移为零,外力做功为零 |
| B.小球从A上升到C与从C上升到B的过程,减少的动能相等 |
| C.小球从A上升到C与从C上升到B的过程,速度的变化率相等 |
| D.小球从A上升到C与从C上升到B的过程,损失的机械能相等 |
用长为l、不可伸长的细线把质量为m的小球悬挂于O点,将小球拉至悬线偏离竖直方向α角后放手,运动t时间后停在最低点。则在时间t内( )
| A.小球重力做功为mgl(1-cosα) |
| B.空气阻力做功为-mglcosα |
| C.小球所受合力做功为mglsinα |
D.绳拉力做功的功率为 |
如图所示,匀强电场水平向左,带正电物体沿绝缘、粗糙水平板向右运动,经A点时动能为100J,到B点时动能减少到80J.减少的动能中有12J转化为电势能,则它再经过B点时,动能大小是( ) 
| A.4J | B.16J | C.32J | D.64J |
如图所示,实线为电场线,虚线为等势线,且相邻两条等势线间的电势差相等。一正电荷(只在电场力的作用下)在φ3上时,具有的动能是20eV,它运动到等势线φ1上时,速度为零。令φ2=0。那么该电荷的电势能为4 eV时,其动能大小为: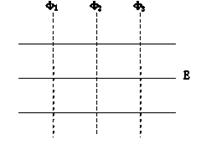
| A.16eV | B.6eV | C.10eV | D.4eV |
图甲是回旋加速器的工作原理图。D1和D2是两个中空的半圆金属盒,它们之间有一定的电势差,A处的粒子源产生的带电粒子,在两盒之间被电场加速。两半圆盒处于与盒面垂直的匀强磁场中,所以粒子在半圆盒中做匀速圆周运动。若带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,不计带电粒子在电场中的加速时间,不考虑由相对论效应带来的影响,下列判断正确的是 
| A.在Ek-t图中应该有tn+1- tn =tn-tn-1 |
| B.在Ek-t图中应该有tn+1- tn <tn-tn-1 |
| C.在Ek-t图中应该有En+1- En =En-En-1 |
| D.在Ek-t图中应该有En+1-En <En-En-1 |
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态。现给小球一竖直向上的初速度,小球最高能运动到M点。在小球从开始运动到运动至最高点时,以下说法正确的是 
| A.小球电势能的减少量大于小球重力势能的增加量 |
| B.小球机械能的改变量等于电场力做的功 |
| C.小球动能的减少量等于电场力和重力做功的代数和 |
| D.弹簧弹性势能的增加量等于小球动能的减少量 |
把导体匀速拉上斜面,如图所示,则下列说法正确的是(不计棒和导轨的电阻,且接触面光滑,匀强磁场磁感应强度B垂直框面向上)( )
| A.拉力做的功等于棒的机械能的增量 |
| B.拉力对棒做的功等于棒的动能的增量 |
| C.拉力与棒受到的磁场力的合力为零 |
| D.拉力对棒做的功与棒克服重力做的功之差等于回路中产生电能 |
光滑斜面上有一个小球自高为h的A处由静止开始滚下,到达光滑的水平面上的B点时速率为V0.光滑水平面上每隔相等的距离设置了一个与小球运动方向垂直的阻挡条,如图所示,小球越过n条阻挡条后停下来.若让小球从2h高处以初速度V0滚下,则小球能越过阻挡条的条数为(设小球每次越过阻挡条时损失的动能相等) :
| A.n | B.2n | C.3n | D.4n |