如图所示,物体P用两根长度相等不可伸长的细线系于竖直杆上,它们随杆转动,若转动角速度为ω,则下列说法错误的是
| A.ω只有超过某一值时,绳子AP才有拉力 |
| B.线BP的拉力随ω的增大而增大 |
| C.线BP的拉力一定大于线AP的拉力 |
| D.当ω增大到一定程度时,线AP的拉力将大于BP的拉力 |
火车转弯做圆周运动,如果外轨和内轨一样高,火车能匀速通过弯道做圆周运动,下列说法中正确的是( )
| A.火车通过弯道向心力的来源是外轨的水平弹力,所以外轨容易磨损 |
| B.火车通过弯道向心力的来源是内轨的水平弹力,所以内轨容易磨损 |
| C.火车通过弯道向心力的来源是火车的重力,所以内外轨道均不磨损 |
| D.以上三种说法都是错误的 |
2010年2月16日,在加拿大城市温哥华举行的第二十一届冬奥会花样滑冰双人自由滑比赛落下帷幕,中国选手申雪、赵宏博获得冠军.如图所示,赵宏博以自己为转动轴拉着申雪做匀速圆周运动.若赵宏博的转速为30 r/min,手臂与竖直方向的夹角为60°,申雪的质量是50 kg,则下列说法正确的是
| A.申雪做圆周运动的角速度为π rad/s |
| B.申雪做圆周运动的角速度为π/2 rad/s |
| C.赵宏博手臂拉力约是850 N |
| D.赵宏博手臂拉力约是1000 N |
火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定。若在某转弯处规定行驶的速度为v,则下列说法中错误的是:( )
| A.当速度大于v时,轮缘挤压外轨 |
| B.当速度小于v时,轮缘挤压外轨 |
| C.当以v的速度通过此弯路时,轮缘既不挤压外轨,也不挤压内轨 |
| D.当以v的速度通过此弯路时,火车重力与轨道支持力的合力提供向心力 |
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最高点P时的速度大小为 ,则以下判断正确的是( )
,则以下判断正确的是( )
| A.小球在P点所受支持力为零 |
B.小球在P点所受支持力不为零但小于 |
C.小球在P点所受支持力等于 |
D.小球在P点所受支持力大于 |
如图所示,长0.5 m的轻质细杆,一端固定有一个质量为3 kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2 m/s,取重力加速度g="10" m/s2,下列说法正确的是 ( )
| A.小球通过最高点时,对杆的拉力大小是24 N |
| B.小球通过最高点时,对杆的压力大小是6 N |
| C.小球通过最低点时,对杆的拉力大小是24 N |
| D.小球通过最低点时,对杆的拉力大小是72 N |
某同学为感受向心力的大小与那些因素有关,做了一个小实验:绳的一端拴一小球,手牵着在空中甩动,使小球在水平面内作圆周运动(如图所示),则下列说法中正确的是( )
| A.保持绳长不变,增大角速度,绳对手的拉力将不变 |
| B.保持绳长不变,增大角速度,绳对手的拉力将增大 |
| C.保持角速度不变,增大绳长,绳对手的拉力将不变 |
| D.保持角速度不变,增大绳长,绳对手的拉力将减小 |
如图所示,用一连接体一端与一小球相连,绕过O点的水平轴在竖直平面内做圆周运动,设轨道半径为r,图中P、Q两点分别表示小球轨道的最高点和最低点,则以下说法正确的是
| A.若连接体是轻质细绳时,小球到达P点的速度可以为零 |
| B.若连接体是轻质细杆时,小球到达P点的速度一定不能为零 |
| C.若连接体是轻质细绳时,小球在P点受到细绳的拉力一定为零 |
| D.若连接体是轻质细杆时,若小球在P点受到细杆的作用力为拉力,在Q点受到细杆的作用力也为拉力 |
铁路在弯道处的内外轨道高度是不同的,如图5所示,已知内外轨道平面对水平面倾角为θ,弯道处的圆弧半径为R,若质量为m的火车转弯时速度小于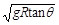 ,则
,则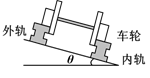
| A.内轨对内侧车轮轮缘有挤压 |
| B.外轨对外侧车轮轮缘有挤压 |
C.这时铁轨对火车的支持力等于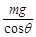 |
D.这时铁轨对火车的支持力等于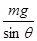 |