题目内容
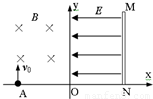
如图所示,坐标平面的第Ⅰ象限内存在大小为E、方向水平向左的匀强电场,第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.足够长的挡板MN垂直x轴放置且距原点O的距离为d.一质量为m、带电量为-q的粒子若自距原点O为L的A点第一次以大小为v,方向沿y轴正方向的速度进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点第二次进入磁场,但初速度大小为2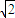 v,为使粒子进入电场后能垂直打在挡板上,求粒子(不计重力)在A点第二次进入磁场时:
v,为使粒子进入电场后能垂直打在挡板上,求粒子(不计重力)在A点第二次进入磁场时:(1)其速度方向与x轴正方向之间的夹角.
(2)粒子到达挡板上时的速度大小及打到挡板MN上的位置到x轴的距离.
【答案】分析:以V进入时半经为 为参考条件,求得以
为参考条件,求得以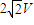 进入时的半径,并由垂直进入电场确定出圆心在Y轴上,画出运动轨迹图,以求得夹角;确定具体运动过程后,可由动能定理求得距离.
进入时的半径,并由垂直进入电场确定出圆心在Y轴上,画出运动轨迹图,以求得夹角;确定具体运动过程后,可由动能定理求得距离.
解答:解: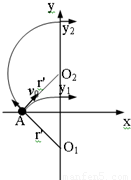 设速度为v时进入磁场后做圆周运动的半径为r
设速度为v时进入磁场后做圆周运动的半径为r
有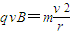 得r=
得r=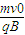 =
=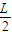
设速度为2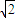 v0时进入磁场做圆周运动的半径r′
v0时进入磁场做圆周运动的半径r′
得r′= =
=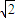 L
L
设其速度方向与x轴正方向之间的夹角为θ
由图中的几何关系有:cosθ=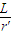 =
=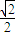 得θ=45°或θ=135°
得θ=45°或θ=135°
(2)为使粒子进入电场后能垂直打在挡板上,则要求粒子进入电场时速度方向与x轴正方向平行,如图所示.粒子进入电场后由动能定理有
qEd= mv′2-
mv′2- m(2
m(2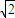 v)2
v)2
得v′=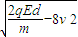
当θ1=45°时,粒子打到挡板MN上的位置到x轴的距离为
y1=r′-r′sin45°=(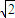 -1)L
-1)L
当θ2=135°时,粒子打到挡板MN上的位置到x轴的距离为
y2=r′+r′sin45°=(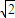 +1)L
+1)L
答:(1)其速度方向与x轴正方向之间的夹角为θ=45°或θ=135°.
(2)粒子到达挡板上时的速度为:v′=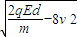
打到挡板MN上的位置到x轴的距离为:(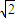 -1)L 或 (
-1)L 或 (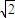 +1)L.
+1)L.
点评:明确求解过程:先定圆心,由条件得半径,确定运动轨迹,有过程后应用动能定理进行解析.
 为参考条件,求得以
为参考条件,求得以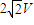 进入时的半径,并由垂直进入电场确定出圆心在Y轴上,画出运动轨迹图,以求得夹角;确定具体运动过程后,可由动能定理求得距离.
进入时的半径,并由垂直进入电场确定出圆心在Y轴上,画出运动轨迹图,以求得夹角;确定具体运动过程后,可由动能定理求得距离.解答:解:
 设速度为v时进入磁场后做圆周运动的半径为r
设速度为v时进入磁场后做圆周运动的半径为r有
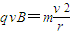 得r=
得r=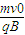 =
=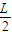
设速度为2
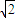 v0时进入磁场做圆周运动的半径r′
v0时进入磁场做圆周运动的半径r′得r′=
 =
=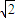 L
L 设其速度方向与x轴正方向之间的夹角为θ
由图中的几何关系有:cosθ=
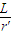 =
=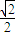 得θ=45°或θ=135°
得θ=45°或θ=135° (2)为使粒子进入电场后能垂直打在挡板上,则要求粒子进入电场时速度方向与x轴正方向平行,如图所示.粒子进入电场后由动能定理有
qEd=
 mv′2-
mv′2- m(2
m(2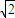 v)2
v)2 得v′=
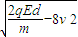
当θ1=45°时,粒子打到挡板MN上的位置到x轴的距离为
y1=r′-r′sin45°=(
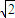 -1)L
-1)L 当θ2=135°时,粒子打到挡板MN上的位置到x轴的距离为
y2=r′+r′sin45°=(
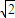 +1)L
+1)L 答:(1)其速度方向与x轴正方向之间的夹角为θ=45°或θ=135°.
(2)粒子到达挡板上时的速度为:v′=
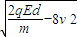
打到挡板MN上的位置到x轴的距离为:(
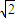 -1)L 或 (
-1)L 或 ( +1)L.
+1)L.点评:明确求解过程:先定圆心,由条件得半径,确定运动轨迹,有过程后应用动能定理进行解析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012?丹东模拟)如图所示,坐标平面的第I象限内存在大小为E、方向水平向左的匀强电场,足够长的挡板MN垂直x轴放置且距离点O为d,第II象限内存在垂直于纸面向里的匀强磁场,磁感应强度为B.一质量为m,带电量为-q的粒子(重力忽略不计)若自距原点O为L的A点以一定的速度垂直x轴进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点进入磁场,但初速度大小为原来的4倍,为使粒子进入电场后能垂直到达挡板MN上,求:
(2012?丹东模拟)如图所示,坐标平面的第I象限内存在大小为E、方向水平向左的匀强电场,足够长的挡板MN垂直x轴放置且距离点O为d,第II象限内存在垂直于纸面向里的匀强磁场,磁感应强度为B.一质量为m,带电量为-q的粒子(重力忽略不计)若自距原点O为L的A点以一定的速度垂直x轴进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点进入磁场,但初速度大小为原来的4倍,为使粒子进入电场后能垂直到达挡板MN上,求:
