题目内容
 如图所示,在光滑斜面上有一重为G的物体,当沿斜面向上和沿水平方向向右各加一个大小为G/2的力于物体时,物体正好静止,如图,则斜面倾角θ为________,斜面所受的压力为________.
如图所示,在光滑斜面上有一重为G的物体,当沿斜面向上和沿水平方向向右各加一个大小为G/2的力于物体时,物体正好静止,如图,则斜面倾角θ为________,斜面所受的压力为________.
53° G
分析:解答该题首先要对物体进行正确的受力分析,物体受到4个力的作用,沿斜面方向建立直角坐标系,把不在坐标轴上的力正交分解,根据受力平衡沿两个坐标轴的方向列式求解,可得出答案.
解答: 解:对物体进行受力分析,受竖直向下的重力G、水平向右的力F、沿斜面向上的力F和垂直于斜面向上的支持力N的作用,沿斜面方向和垂直于斜面的方向建立直角坐标系,把不在坐标轴上的力正交分解,因物体静止,处于共点力平衡状态,所以有:
解:对物体进行受力分析,受竖直向下的重力G、水平向右的力F、沿斜面向上的力F和垂直于斜面向上的支持力N的作用,沿斜面方向和垂直于斜面的方向建立直角坐标系,把不在坐标轴上的力正交分解,因物体静止,处于共点力平衡状态,所以有:
沿x轴方向:Gsinθ=F+Fcosθ
因F= ,整理的:
,整理的:
 ,可得:θ=53°
,可得:θ=53°
沿y轴方向:N=Gcosθ+Fsinθ
将θ=53°和F= 代入上式得:N=G×0.6+
代入上式得:N=G×0.6+ ×0.8=G
×0.8=G
故答案为:53°,G
点评:该题考查了物体在多个共点力的作用下处于平衡的问题,解决此类问题往往是先建立直角坐标系,把不在坐标系上的力进行正交分解,沿两个坐标轴的方向列式求解.
建立直角坐标系原则上方向是任意的,但为了解题方便,注意以下几条:
①将尽可能多的力放到坐标轴上,这样可以减少需要分解的力的个数;
②若物体在斜面上,常常让一条坐标轴沿着斜面方向;
③若物体具有加速度,往往让一条坐标轴沿着合外力的方向(即为加速度方向).
分析:解答该题首先要对物体进行正确的受力分析,物体受到4个力的作用,沿斜面方向建立直角坐标系,把不在坐标轴上的力正交分解,根据受力平衡沿两个坐标轴的方向列式求解,可得出答案.
解答:
 解:对物体进行受力分析,受竖直向下的重力G、水平向右的力F、沿斜面向上的力F和垂直于斜面向上的支持力N的作用,沿斜面方向和垂直于斜面的方向建立直角坐标系,把不在坐标轴上的力正交分解,因物体静止,处于共点力平衡状态,所以有:
解:对物体进行受力分析,受竖直向下的重力G、水平向右的力F、沿斜面向上的力F和垂直于斜面向上的支持力N的作用,沿斜面方向和垂直于斜面的方向建立直角坐标系,把不在坐标轴上的力正交分解,因物体静止,处于共点力平衡状态,所以有:沿x轴方向:Gsinθ=F+Fcosθ
因F=
 ,整理的:
,整理的: ,可得:θ=53°
,可得:θ=53°沿y轴方向:N=Gcosθ+Fsinθ
将θ=53°和F=
 代入上式得:N=G×0.6+
代入上式得:N=G×0.6+ ×0.8=G
×0.8=G故答案为:53°,G
点评:该题考查了物体在多个共点力的作用下处于平衡的问题,解决此类问题往往是先建立直角坐标系,把不在坐标系上的力进行正交分解,沿两个坐标轴的方向列式求解.
建立直角坐标系原则上方向是任意的,但为了解题方便,注意以下几条:
①将尽可能多的力放到坐标轴上,这样可以减少需要分解的力的个数;
②若物体在斜面上,常常让一条坐标轴沿着斜面方向;
③若物体具有加速度,往往让一条坐标轴沿着合外力的方向(即为加速度方向).

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
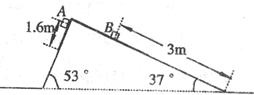 (2010?青岛三模)如图所示,一光滑斜面固定在水平面上,斜面上放置一质量不计的柔软薄纸带.现将质量为mA的物体A和质量mB的物体B轻放在纸带上.两物体可视为质点,物体初始位置数据如图所示,A到纸带末端的距离为而x1=l.6m,B放在纸带上距离底端x2=3m.
(2010?青岛三模)如图所示,一光滑斜面固定在水平面上,斜面上放置一质量不计的柔软薄纸带.现将质量为mA的物体A和质量mB的物体B轻放在纸带上.两物体可视为质点,物体初始位置数据如图所示,A到纸带末端的距离为而x1=l.6m,B放在纸带上距离底端x2=3m. 如图所示,在光滑斜面上有一重为G的物体,当沿斜面向上和沿水平方向向右各加一个大小为G/2的力于物体时,物体正好静止,如图,则斜面倾角θ为
如图所示,在光滑斜面上有一重为G的物体,当沿斜面向上和沿水平方向向右各加一个大小为G/2的力于物体时,物体正好静止,如图,则斜面倾角θ为 如图所示,在光滑水平面AB上,水平恒力F推动质量为m=1kg的物体从A点由静止开始做匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变,最高能到达C点,用速度传感器测量物体的瞬时速度,表中记录了部分测量数据),求:
如图所示,在光滑水平面AB上,水平恒力F推动质量为m=1kg的物体从A点由静止开始做匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变,最高能到达C点,用速度传感器测量物体的瞬时速度,表中记录了部分测量数据),求: