题目内容
18. 如图所示,小木块的质量m=0.4kg,以速度v0=20m/s水平地滑上一个静止的平板小车,小车的质量M=1.6kg,小木块与小车间的动摩擦因数μ=0.2(不计车与路面的摩擦,g=10m/s2).求:
如图所示,小木块的质量m=0.4kg,以速度v0=20m/s水平地滑上一个静止的平板小车,小车的质量M=1.6kg,小木块与小车间的动摩擦因数μ=0.2(不计车与路面的摩擦,g=10m/s2).求:(1)小车的加速度a为多少?
(2)小木块相对于小车静止时,小车的速度v为多少?
(3)小木块滑上小车到相对于小车静止所经历的时间t为多少?
分析 (1)对平板车进行受力分析,它都只受到滑动摩擦力的作用,根据牛顿第二定律求出加速度;
(2)木块和小车组成的系统,所受合力为零,动量保持不变,根据动量守恒定律求出共同速度;
(3)木块和小车相对静止时小车的速度大小.以木块为研究对象,根据动量定理求出时间.
解答 解:(1)对平板车,μmg=Ma2,
代入数据解得a2=0.5m/s2
(2)以木块和小车为研究对象,向右方向为正方向,由动量守恒定律可得:
mv0=(M+m)v
得v=$\frac{m{v}_{0}}{M+m}=\frac{0.4×20}{1.6+0.4}=4$m/s
(3)以木块为研究对象,由动量定理可得
-ft=mv-mv0
又f=μmg
得到t=$\frac{0.4×(20-4)}{0.2×0.4×10}=8$s
答:(1)小车的加速度a为0.5m/s2
(2)小木块相对于小车静止时,小车的速度v为4m/s;
(3)小木块滑上小车到相对于小车静止所经历的时间t为8s.
点评 该题是相对运动的典型例题,要认真分析两个物体的受力情况,正确判断两物体的运动情况,要掌握动量守恒定律和能量守恒的应用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
9. 图示为转轮传动装置,传动过程中没有打滑现象,A、B、C三点的位置关系如图,若O1C=r2,则三点的向心加速度的关系为( )
图示为转轮传动装置,传动过程中没有打滑现象,A、B、C三点的位置关系如图,若O1C=r2,则三点的向心加速度的关系为( )
 图示为转轮传动装置,传动过程中没有打滑现象,A、B、C三点的位置关系如图,若O1C=r2,则三点的向心加速度的关系为( )
图示为转轮传动装置,传动过程中没有打滑现象,A、B、C三点的位置关系如图,若O1C=r2,则三点的向心加速度的关系为( )| A. | aA=aB=aC | B. | aC<aA<aB | C. | aC>aA>aB | D. | aC=aB>aA |
6.如图所示,A、B两灯相同,L是带铁芯的电阻可不计的线圈,下列说法中正确的是( )

| A. | 开关K合上瞬间,A灯先亮 B灯后亮 | |
| B. | K合上稳定后,A、B同时亮着 | |
| C. | K断开瞬间,A、B同时熄灭 | |
| D. | K断开瞬间,B立即熄灭,A闪亮一下再熄灭 |
13.机械手表中的分针和秒针在转动时,可视为匀速运动.分针和秒针从重合开始到第2次重合,中间经历时间为( )min.
| A. | 1 | B. | $\frac{59}{60}$ | C. | $\frac{60}{59}$ | D. | $\frac{61}{60}$ |
3.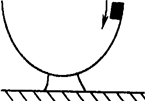 质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )
质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )
 质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )
质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )| A. | 因为速率不变,所以木块的加速度为零 | |
| B. | 木块下滑过程中所受的合外力越来越大 | |
| C. | 木块下滑过程中所受的摩擦大小不变 | |
| D. | 木块下滑过程中的加速度大小不变,方向始终指向球心 |
10. 材料、粗细相同,长度不同的电阻丝做成ab、cd、ef三种形状的导线,分别放在电阻可忽略的光滑金属导轨上,并与导轨垂直,如图所示,匀强磁场方向垂直导轨平面向内.外力使导线水平向右做匀速运动,且每次外力所做功的功率相同,已知三根导线在导轨间的长度关系是Lab<Lcd<Lef,则( )
材料、粗细相同,长度不同的电阻丝做成ab、cd、ef三种形状的导线,分别放在电阻可忽略的光滑金属导轨上,并与导轨垂直,如图所示,匀强磁场方向垂直导轨平面向内.外力使导线水平向右做匀速运动,且每次外力所做功的功率相同,已知三根导线在导轨间的长度关系是Lab<Lcd<Lef,则( )
 材料、粗细相同,长度不同的电阻丝做成ab、cd、ef三种形状的导线,分别放在电阻可忽略的光滑金属导轨上,并与导轨垂直,如图所示,匀强磁场方向垂直导轨平面向内.外力使导线水平向右做匀速运动,且每次外力所做功的功率相同,已知三根导线在导轨间的长度关系是Lab<Lcd<Lef,则( )
材料、粗细相同,长度不同的电阻丝做成ab、cd、ef三种形状的导线,分别放在电阻可忽略的光滑金属导轨上,并与导轨垂直,如图所示,匀强磁场方向垂直导轨平面向内.外力使导线水平向右做匀速运动,且每次外力所做功的功率相同,已知三根导线在导轨间的长度关系是Lab<Lcd<Lef,则( )| A. | ab运动速度最大 | |
| B. | ef运动速度最大 | |
| C. | 三根导线每秒产生的热量相同 | |
| D. | 因三根导线切割磁感线的有效长度相同,故它们产生的感应电动势相同 |
8. 攀岩是从登山运动中衍生出来的竞技运动项目,50年代起源于苏联,是军队中作为一个军事训练项目而存在的,如图,一个运动员正沿着一根固定的绳子往上爬越一大岩石,则( )
攀岩是从登山运动中衍生出来的竞技运动项目,50年代起源于苏联,是军队中作为一个军事训练项目而存在的,如图,一个运动员正沿着一根固定的绳子往上爬越一大岩石,则( )
 攀岩是从登山运动中衍生出来的竞技运动项目,50年代起源于苏联,是军队中作为一个军事训练项目而存在的,如图,一个运动员正沿着一根固定的绳子往上爬越一大岩石,则( )
攀岩是从登山运动中衍生出来的竞技运动项目,50年代起源于苏联,是军队中作为一个军事训练项目而存在的,如图,一个运动员正沿着一根固定的绳子往上爬越一大岩石,则( )| A. | 人越往上爬,绳子的张力越大 | B. | 人越往上爬,绳子的张力越小 | ||
| C. | 人越往上爬,人腿部承受的力越大 | D. | 人越往上爬,人腿部承受的力越小 |
 如图,匀强电场的场强为103V/m,a、b两点间的距离为0.1m,ab连线与电场方向的夹角为60°,则a、b两点间的电势差为50V,若将电量为-2×10-10C的点电荷从a点移到b点,电场力做功为1×10-8 J.
如图,匀强电场的场强为103V/m,a、b两点间的距离为0.1m,ab连线与电场方向的夹角为60°,则a、b两点间的电势差为50V,若将电量为-2×10-10C的点电荷从a点移到b点,电场力做功为1×10-8 J. 如图所示,两竖直放置的平行光滑导轨处于垂直于导轨平面的匀强磁场中,金属杆ab可沿导轨滑动,金属杆ab始终与导轨接触良好且保持水平,原先S断开,让ab杆由静止下滑,一段时间后闭合S,则从S闭合开始记时,ab杆的运动速度v随时间t的关系图不可能是下图中的哪一个?( )
如图所示,两竖直放置的平行光滑导轨处于垂直于导轨平面的匀强磁场中,金属杆ab可沿导轨滑动,金属杆ab始终与导轨接触良好且保持水平,原先S断开,让ab杆由静止下滑,一段时间后闭合S,则从S闭合开始记时,ab杆的运动速度v随时间t的关系图不可能是下图中的哪一个?( )


