题目内容
如图所示，扇形AOB为透明柱状介质的横截面，半径为R，介质折射率为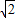
，圆心角∠AOB=90°，MN为其对称轴，一束平行于对称轴的单色光由OA面射入介质．要使柱体AB面没有光线射出，需在O点垂直于对称轴MN放置一遮光板，则遮光板的长度至少为（ ）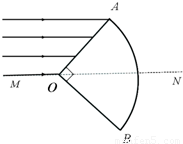
A．
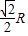
B．
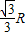
C．
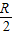
D．
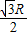
【答案】分析：根据折射定律和全反射定理求出各角的大小，由正弦定理和三角形知识求挡板的高度．
解答：解：设在OA面上的一点P入射的光线恰好不能从AB面射出，经过折射在AB面的N点方式全反射．
由几何关系可知光从P点射入时的入射角θ=45°，由折射定律：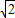
=
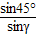，得折射角为：∠γ=30°，要使光不能从AB面射出，在D点的入射角等于45°
由几何关系知，∠OPD=120°，∠PDO=45°，
由正弦定理：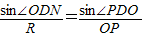
，遮光板的长度至少为L=OPsin45°=
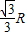，B正确．
故选B
点评：本题考查折射定律及全反射规律，以及学生运用数学处理物理问题的能力．
解答：解：设在OA面上的一点P入射的光线恰好不能从AB面射出，经过折射在AB面的N点方式全反射．
由几何关系可知光从P点射入时的入射角θ=45°，由折射定律：
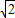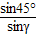=，得折射角为：∠γ=30°，要使光不能从AB面射出，在D点的入射角等于45°由几何关系知，∠OPD=120°，∠PDO=45°，
由正弦定理：
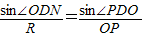，遮光板的长度至少为L=OPsin45°=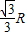，B正确．故选B
点评：本题考查折射定律及全反射规律，以及学生运用数学处理物理问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，扇形AOB为透明柱状介质的横截面，半径为R，介质折射率为
（选修3-4）
如图所示，扇形AOB为透明柱状介质的横截面，圆心角∠AOB=60°，一束平行于角平分线OM的单色光由OA射入介质，经OA折算的光线恰平行于OB．
如图所示，扇形AOB为透明柱状介质的横截面，圆心角∠AOB=60°．一束平行于角平分线OM的单色光由叫射人介质，经OA折射的光线恰平行于OB．
如图所示，扇形AOB为透明柱状介质的横截面，半径为R，介质折射率为