��Ŀ����
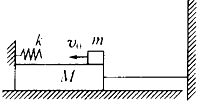 ��ͼ��ʾ������ΪM�ij����龲ֹ�ڹ⻬ˮƽ���ϣ����̶�һ����ϵ��k�㹻���ˮƽ���ʵ��ɣ��Ҳ���һ�����쳤��ϸ������������ֱǽ�ϣ�ϸ�����ܳ��ܵ��������ΪT��ʹһ����Ϊm�����ٶ�Ϊv0��С��飬�ڻ�������Ħ��������������ѹ�����ɣ������ɵ������ܵı���ʽEp=
��ͼ��ʾ������ΪM�ij����龲ֹ�ڹ⻬ˮƽ���ϣ����̶�һ����ϵ��k�㹻���ˮƽ���ʵ��ɣ��Ҳ���һ�����쳤��ϸ������������ֱǽ�ϣ�ϸ�����ܳ��ܵ��������ΪT��ʹһ����Ϊm�����ٶ�Ϊv0��С��飬�ڻ�������Ħ��������������ѹ�����ɣ������ɵ������ܵı���ʽEp=| 1 |
| 2 |
��1������ϸ�������ϵ�������
��2��������ϸ�����Ϻ��ٵĹ����У����ܻ�õ����������ٶ�Ϊ���٣�
��3����֤������������뿪����ʱ����Ե��治�����˶���������v0��
| T | ||
|
��������1��ϸ��ǡ�ñ�����ʱ��ϸ��������ǡ�õ���T�����ݺ��˶���������ɵ�ѹ�������ڵ��ɱ�ѹ���Ĺ����У����Ķ���ת��Ϊ���ɵĵ������ܣ��ɻ�е���غ����ϸ��������ʱ�����ٶ�������
��2��������ϸ�����Ϻ��ٵĹ����У�����������˶����������������˶����������ٶ���ͬʱ������ѹ��ʱx���M��õļ��ٶ������ϵͳ�����غ�ͻ�е���غ�����������ѹ����������ţ�ٵڶ��������M���ļ��ٶȣ�
��3����������뿪����ʱ����Ե��治�����˶�������Ե�����ٶ�Ϊ�㣬����ϵͳ�����غ�ͻ�е���غ���ʽ�����v0��������
��2��������ϸ�����Ϻ��ٵĹ����У�����������˶����������������˶����������ٶ���ͬʱ������ѹ��ʱx���M��õļ��ٶ������ϵͳ�����غ�ͻ�е���غ�����������ѹ����������ţ�ٵڶ��������M���ļ��ٶȣ�
��3����������뿪����ʱ����Ե��治�����˶�������Ե�����ٶ�Ϊ�㣬����ϵͳ�����غ�ͻ�е���غ���ʽ�����v0��������
����⣺��1����ϸ���ձ�����ʱ���ɵ�ѹ����Ϊx0����ʱ�� kx0=T
Ϊʹ����ѹ���ﵽx0����С���Ҫ����
m
��
k
�ɴ˵õ���ϸ�������ϵ������ǣ�v0��
��2������ʱ��С�����ٶ�Ϊv1������
m
=
m
+
k
��kx0=T
���v1=
����M�ڵ����������ɾ�ֹ��ʼ���٣�ֱ����m�ﵽ��ͬ�ٶ�v2����ʱ����ѹ��ʱx������ɶ����غ�ͻ�е���غ��
mv1=��M+mv2
m
=
(M+m)
+
kx2
��ʱM�ļ��ٶ����Ϊ a=
�������a=
��3��ľ����С����ͨ�������������ʱ����Ե���ǡ�ò������˶�ʱ��С������Ե�����ٶ�ӦΪ0�����ʱľ����ٶ�ΪV1������С����ѹ������ǰ���ٶ�Ϊv0�䣬����˲��С������ٶ�Ϊv1������ mv=MV1
m(v0��)2=
M
���Ͻ��С��������뿪ľ��ʱ����Ե����ٶ�Ϊ�������
v0��=
����m��M
������������뿪����ʱ����Ե��治�����˶���������v0��
����m��M��
�𣺣�1��ϸ�������ϵ���������v0��
��
��2��������ϸ�����Ϻ��ٵĹ����У����ܻ�õ����������ٶ�Ϊ��a=
��
��3��֤�����ϣ�
Ϊʹ����ѹ���ﵽx0����С���Ҫ����
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| x | 2 0 |
�ɴ˵õ���ϸ�������ϵ������ǣ�v0��
| T | ||
|
��2������ʱ��С�����ٶ�Ϊv1������
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| x | 2 0 |
��kx0=T
���v1=
|
����M�ڵ����������ɾ�ֹ��ʼ���٣�ֱ����m�ﵽ��ͬ�ٶ�v2����ʱ����ѹ��ʱx������ɶ����غ�ͻ�е���غ��
mv1=��M+mv2
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
��ʱM�ļ��ٶ����Ϊ a=
| kx |
| M |
�������a=
| 1 |
| M |
|
��3��ľ����С����ͨ�������������ʱ����Ե���ǡ�ò������˶�ʱ��С������Ե�����ٶ�ӦΪ0�����ʱľ����ٶ�ΪV1������С����ѹ������ǰ���ٶ�Ϊv0�䣬����˲��С������ٶ�Ϊv1������ mv=MV1
| 1 |
| 2 |
| 1 |
| 2 |
| V | 2 1 |
���Ͻ��С��������뿪ľ��ʱ����Ե����ٶ�Ϊ�������
v0��=
| T | ||
|
������������뿪����ʱ����Ե��治�����˶���������v0��
| T | ||
|
�𣺣�1��ϸ�������ϵ���������v0��
| T | ||
|
��2��������ϸ�����Ϻ��ٵĹ����У����ܻ�õ����������ٶ�Ϊ��a=
| 1 |
| M |
|
��3��֤�����ϣ�
������������ϵͳ�����غ�ͻ�е���غ���ۺ�Ӧ�ã�Ҫ�ھ����������ٽ�������ϸ�������ϸպñ�����ʱ��ϸ���������ﵽ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
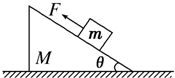 ��ͼ��ʾ������ΪM��Ш����龲ֹ��ˮƽ�����ϣ���б������Ϊ�ȣ�б������һ����Ϊm��С��飬С�����б��֮�����Ħ�����ú���F��б����������ʹ֮�����ϻ�����С����˶��Ĺ����У�Ш�����ʼ�ձ��־�ֹ��������
��ͼ��ʾ������ΪM��Ш����龲ֹ��ˮƽ�����ϣ���б������Ϊ�ȣ�б������һ����Ϊm��С��飬С�����б��֮�����Ħ�����ú���F��б����������ʹ֮�����ϻ�����С����˶��Ĺ����У�Ш�����ʼ�ձ��־�ֹ��������| A�������Ш������֧����Ϊ��M+m��g | B�������Ш������Ħ����Ϊ�� | C��Ш������С���Ħ��������Ϊ�� | D��С���һ���ܵ��ĸ������� |
 ��ͼ��ʾ������ΪM��б�������ˮƽ���ϣ�����������Ϊm��С��飬���Ӵ������Ħ��������һ�ν�ˮƽ��F1����M�ϣ��ڶ��ν�F2����m�ϣ����ζ�Ҫ��m��M��������Ի�������F1��F2�ı�Ϊ��������
��ͼ��ʾ������ΪM��б�������ˮƽ���ϣ�����������Ϊm��С��飬���Ӵ������Ħ��������һ�ν�ˮƽ��F1����M�ϣ��ڶ��ν�F2����m�ϣ����ζ�Ҫ��m��M��������Ի�������F1��F2�ı�Ϊ�������� ��ͼ��ʾ������Ϊm��С��ˮƽ���Ϊ2mʱ���ٶȵĴ�СΪ4m/s��������ֱ���£�������˶��п��������Ĵ�С����������0.1��������������Ĺ����в���ʧ��е�ܣ���
��ͼ��ʾ������Ϊm��С��ˮƽ���Ϊ2mʱ���ٶȵĴ�СΪ4m/s��������ֱ���£�������˶��п��������Ĵ�С����������0.1��������������Ĺ����в���ʧ��е�ܣ��� ��ͼ��ʾ������Ϊm��С��A���ɾ�ֹ��ʼ�������䣬���ٶȴ�СΪ
��ͼ��ʾ������Ϊm��С��A���ɾ�ֹ��ʼ�������䣬���ٶȴ�СΪ ��ͼ��ʾ������ΪM����ͨ�������ֽ�����Ϊm�������Լ��ٶ�a���ᣬ�����������̣��˱��־�ֹ����������ֱ����н�Ϊ�ȣ���
��ͼ��ʾ������ΪM����ͨ�������ֽ�����Ϊm�������Լ��ٶ�a���ᣬ�����������̣��˱��־�ֹ����������ֱ����н�Ϊ�ȣ���