题目内容
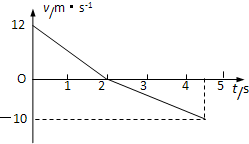 一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜
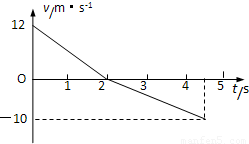
一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜面底端时的速度大小为10m/s,在此全过程中的v-t图象如图所示,求:
(1)斜面的长度L;
(2)物体从斜面顶端滑到底端所用的时间t;
(3)斜面的倾角θ的正弦值sinθ=?
(4)物体在斜面上运动时受到斜面给它的滑动摩擦力大小是物体所受重力大小的几倍.
分析:速度时间图象与坐标轴围成的面积表示位移,斜率表示加速度,根据牛顿第二定律及运动学基本公式即可解题.
解答:解:(1)由图象得斜面的长度
L=
t1=
×2m=12m
(2)下滑过程由L=
t2
得物体从斜面顶端滑到底端所用的时间t=2.4s
(3)上滑过程的加速度a1=
解得:a1=6m/s2
由牛顿第二定律得mgsinθ+Ff=ma1
下滑过程中的加速度大小a2=
a2=
m/s2
由牛顿第二定律得mgsinθ-Ff=ma2
解得sinθ=
Ff=
m…(1分)
(4)所以Ff=
mg,即滑动摩擦力大小是物体所受重力大小的
倍.
答:(1)斜面的长度为12m;
(2)物体从斜面顶端滑到底端所用的时间为2.4s;
(3)斜面的倾角θ的正弦值sinθ=
;
(4)物体在斜面上运动时受到斜面给它的滑动摩擦力大小是物体所受重力大小的
倍.
L=
| v1 |
| 2 |
| 12 |
| 2 |
(2)下滑过程由L=
| v2 |
| 2 |
得物体从斜面顶端滑到底端所用的时间t=2.4s
(3)上滑过程的加速度a1=
| △v1 |
| △t1 |
解得:a1=6m/s2
由牛顿第二定律得mgsinθ+Ff=ma1
下滑过程中的加速度大小a2=
| △v2 |
| △t2 |
a2=
| 25 |
| 6 |
由牛顿第二定律得mgsinθ-Ff=ma2
解得sinθ=
| 61 |
| 120 |
Ff=
| 11 |
| 12 |
(4)所以Ff=
| 11 |
| 120 |
| 11 |
| 120 |
答:(1)斜面的长度为12m;
(2)物体从斜面顶端滑到底端所用的时间为2.4s;
(3)斜面的倾角θ的正弦值sinθ=
| 61 |
| 120 |
(4)物体在斜面上运动时受到斜面给它的滑动摩擦力大小是物体所受重力大小的
| 11 |
| 120 |
点评:本题主要考查了牛顿第二定律及运动学基本公式的直接应用,要求同学们明确图象的面积和斜率的含义,能根据图象得出有用信息,难度适中.

练习册系列答案
相关题目
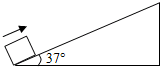 一物体以12m/s的初速度冲上一足够长斜面,然后又沿斜面向下运动,斜面倾角为37°,物体与斜面间的动摩擦因数为0.25,当地重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求
一物体以12m/s的初速度冲上一足够长斜面,然后又沿斜面向下运动,斜面倾角为37°,物体与斜面间的动摩擦因数为0.25,当地重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求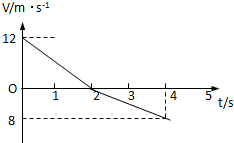 一物体以12m/s的初速度冲上斜面,然后又沿斜面向下运动,在此全过程中的v-t图象如图所示,求
一物体以12m/s的初速度冲上斜面,然后又沿斜面向下运动,在此全过程中的v-t图象如图所示,求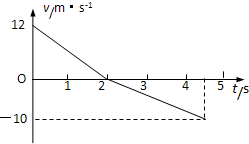 一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜
一物体以12m/s的初速度冲上斜面的最顶端,然后又沿斜面向下运动,返回斜