题目内容
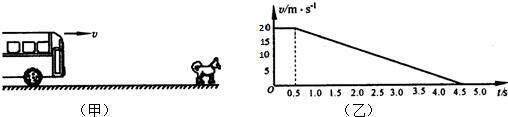
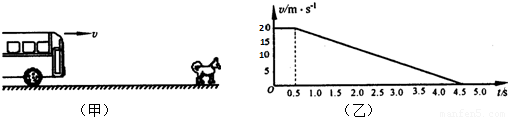
一辆长途客车正在以20m/s的速度匀速行驶．突然，司机看见车的正前方x=33m处有一只狗，如图（甲）所示，司机立即采取制动措施．若从司机看见狗开始计时（t=0），长途客车的“速度-时间”图象如图（乙）所示．（1）求长途客车从司机发现狗至客车停止运动的这段时间内前进的距离；
（2）求长途客车制动时的加速度；
（3）若狗以v′=4m/s的速度与长途客车同向奔跑，狗能否被撞？
【答案】分析：（1）速度图象与时间轴围成的面积等于物体通过的位移．
（2）速度图象的斜率等于物体的加速度．
（3）要避免客车与狗相撞，则客车追上狗时客车的速度等于狗的速度，求出狗的位移和客车的位移的关系即可确定能否追上．利用速度位移的关系式vt2-v2=2ax求出客车的位移，根据加速度的定义式a=
求出客车刹车到狗速度的时间以及在此时间内狗通过的位移，根据位移关系即可确定客车是否能够撞上狗．
解答：解：（1）客车在前0.5s内的位移x1=vt1=20×0.5=10m
客车在0.5-4.5s内的位移x2=
（vt2）=
×20×（4.5-0.5）=40m
故客车从司机发现狗至客车停止运动的这段时间内前进的距离x=x1+x2=50m
（2）由图象得：
（3）若客车恰好撞不到狗，则车追上狗时车速为4m/s，
则刹车时间为
客车位移为
而狗通过的位移为x2=v（t1+t）=4×（0.5+3.2）=14.8mx2+33=47.8m
因为x1＞x2+33，所以狗将被撞．
点评：熟练掌握速度图象的物理含义：图象的斜率等于物体的加速度，图象与时间轴围成的面积等于物体通过的位移，这是解决此类题目的基本策略．
（2）速度图象的斜率等于物体的加速度．
（3）要避免客车与狗相撞，则客车追上狗时客车的速度等于狗的速度，求出狗的位移和客车的位移的关系即可确定能否追上．利用速度位移的关系式vt2-v2=2ax求出客车的位移，根据加速度的定义式a=
求出客车刹车到狗速度的时间以及在此时间内狗通过的位移，根据位移关系即可确定客车是否能够撞上狗．解答：解：（1）客车在前0.5s内的位移x1=vt1=20×0.5=10m
客车在0.5-4.5s内的位移x2=
（vt2）=×20×（4.5-0.5）=40m故客车从司机发现狗至客车停止运动的这段时间内前进的距离x=x1+x2=50m
（2）由图象得：
（3）若客车恰好撞不到狗，则车追上狗时车速为4m/s，
则刹车时间为
客车位移为
而狗通过的位移为x2=v（t1+t）=4×（0.5+3.2）=14.8mx2+33=47.8m
因为x1＞x2+33，所以狗将被撞．
点评：熟练掌握速度图象的物理含义：图象的斜率等于物体的加速度，图象与时间轴围成的面积等于物体通过的位移，这是解决此类题目的基本策略．
练习册系列答案
相关题目
