题目内容

18．如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度ω转动，盘面与水平面的夹角为30°，盘面上离转轴距离2.5m处有一小物体与圆盘始终保持相对静止，小物体的质量为1.0kg，小物体与盘面间的动摩擦因数为$\frac{\sqrt{3}}{2}$（设最大静摩擦力等于滑动摩擦力）．则当ω达最大值时，小物体运动到最高点A时所受摩擦力的大小（g取10m/s2）（　　）
A．2.5NB．5NC．7.5ND．10N

分析 根据牛顿第二定律，求出物体在最低点时，角速度的最大值，再根据牛顿第二定律求出物块在最高点A时所受的摩擦力大小．

解答 解：在最低点，当摩擦力达到最大值时，$μmgcos30°-mgsin30°=mr{{ω}_{m}}^{2}$，
在最高点，根据牛顿第二定律得，$f+mgsin30°=mr{{ω}_{m}}^{2}$，
代入数据，联立解得f=-2.5N，负号表示方向，故A正确，B、C、D错误．
故选：A．

点评 解决本题的关键知道小球在最高点和最低点向心力的来源，抓住临界状态，结合牛顿第二定律进行求解．

练习册系列答案
相关题目
1．如图所示为商场安装的智能化台阶式自动扶梯，为了节约能源，在没有乘客乘行时，自动扶梯以较小的速度匀速运行，当有乘客乘行时自动扶梯经过先加速再匀速两个阶段运行，全过程中乘客中乘客与扶梯始终相对静止，则电梯在向上运送乘客的过程中，下列判断正确的是（　　）
A．加速阶段支持力对乘客做正功B．加速阶段摩擦力对乘客做负功
C．匀速阶段合外力对乘客做正功D．匀速阶段乘客的机械能守恒
2．开普勒分别于1609年和1619年发表了他发现的行星运动规律，后人称之为开普勒行星运动定律．火星和木星沿各自的椭圆轨道绕太阳运行，且火星的半长轴大于木星的半长轴．根据开普勒行星运动定律可知（　　）
A．太阳位于火星和木星运行轨道的中心
B．火星绕太阳运动的周期大于木星绕太阳运动的周期
C．对于火星或木星，离太阳越近，运动速率就越大
D．相同时间内，火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积
6．如图所示，竖直放置的气缸内壁有固定支架，支架上方的轻质活塞上堆放有0.25kg的细砂（细砂没有画出），开始时封闭气体的压强为1×105Pa，温度为300K．对气体缓慢加热，使气体温度升高，已知大气压强p0=1×105Pa，活塞的横截面积S=1cm2，g取10m/s2．
i．求活塞刚要离开支架时气体的温度．
ii．在活塞离开支架后缓慢取走活塞上的细砂，同时继续对气体加热保持气体的温度不变，发现全部取走细砂时活塞向上移动了4cm，求活塞最初离气缸底的距离．
13．如图①所示，高空滑索是一种勇敢者的运动项目．如果一个人用轻绳通过轻质滑环悬吊在足够长的倾斜钢索上运动，在下滑过程中可能会出现如图②和如图③所示的两种情形．不计空气阻力，则下列说法不正确的是（　　）
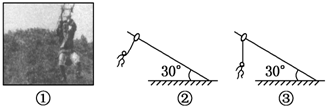
A．图②的情形中，人只能匀加速下滑
B．图②的情形中，钢索对轻环的作用力大小为$\frac{\sqrt{3}}{2}$mg
C．图③的情形中，钢索对轻环无摩擦力
D．图③的情形中，人匀速下滑
3．关于平抛运动，下面说法正确的是（　　）
A．由于物体只受重力作用，因此平抛运动是匀变速运动
B．由于速度的方向不断变化，因此平抛运动不是匀变速运动
C．平抛运动的时间由抛出时的高度和初速度的大小共同决定
D．平抛运动的水平位移由抛出时的高度和初速度的大小共同决定
10．在下列叙述中，正确的是（　　）
A．β衰变中产生的β射线是原子核外电子挣脱原子核束缚后形成的
B．康普顿效应说明光具有波动性
C．玛丽•居里最早发现了天然放射现象
D．重核裂变和轻核聚变都会发生质量亏损释放核能
7．如图所示，当带正电的球C移近不带电的枕形金属导体A端时，下列说法正确的是（　　）
A．枕形金属导体的A端带负电，B端带正电
B．金属导体中的正、负电荷同时分别向B端和A端移动
C．金属导体中的带负电的电子向A端移动，正电荷不移动
D．金属导体中的正电荷向B端移动，带负电的电子不移动
8．暗物质是二十一世纪物理学家之谜，对该问题的研究可能带来了一场物理学家的革命．为了探测暗物质，我国在2015年年12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星．已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动，经过时间t（t小于其运动周期），运动的弧长为s，与地球中心连线扫过的角度为β（弧度），引力常量为G，则下列说法中正确的是（　　）
A．“悟空”的线速度大于第一宇宙速度
B．“悟空”的向心加速度大于地球同步卫星的向心加速度
C．“悟空”的质量为$\frac{{s}^{3}}{G{t}^{2}β}$
D．“悟空”的环绕周期为$\frac{2π}{β}$t

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网