题目内容
半径为R的玻璃半圆柱体,横截面积如图4-1-7所示,圆心为O.两条平行单色红光沿截面射向圆柱面,方向与底面垂直.光线1的入射点A为圆柱的顶点,光线2的入射点为B,∠AOB=60°.已知玻璃对红光的折射率n=3.求:

图4-1-7
(1)两条光线经柱面和底面折射后的交点与O点的距离d;
(2)若入射光是单色的蓝光,则距离d将比上面求得的结果大还是小.
d=![]() R
R
解析:
光线1始终和界面垂直,不发生折射现象,光线2经柱面和底面发生两次折射,画出
光路图,根据折射定律和几何关系即可求出d的大小.
(1)两条光线经柱面和底面折射的光路如图所示.

由折射定律,得:n=![]()
所以sinMBC=![]() ,所以∠MBC=30°.
,所以∠MBC=30°.
又由几何关系知∠OCB=180°-30°-30°=120°,根据正弦定理,得:
![]() 所以OC=
所以OC=![]() R.
R.
同样由几何关系知∠PCB=30°.根据折射定律,得:
n=![]() 解得∠DCQ=60°,所以∠DCO=30°,d=OD=OCtan30°=
解得∠DCQ=60°,所以∠DCO=30°,d=OD=OCtan30°=![]() R.
R.
(2)由于玻璃对蓝光的折射率较大,所以经上述两次折射后,蓝光的偏折角较大,d偏小.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 (2003?广州一模)半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点为B,∠AOB=60°,已知该玻璃对红光的折射率n=
(2003?广州一模)半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点为B,∠AOB=60°,已知该玻璃对红光的折射率n=

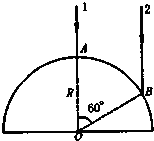 半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点B,∠AOB=60°,已知该玻璃对红光的折射率n=
半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点B,∠AOB=60°,已知该玻璃对红光的折射率n=