题目内容
12. 某同学利用如图实验装置研究摆球的运动情况,摆球由A点由静止释放.经过最低点C到达与A等高的B点,D、E、F是OC连线上的点,OE=ED,DF=FC,OC连接上各点均可钉细钉子,每次均将摆球从A点由静止释放,不计绳与钉子碰撞时机械能的损失,不计空气阻力,下列说法正确的是( )
某同学利用如图实验装置研究摆球的运动情况,摆球由A点由静止释放.经过最低点C到达与A等高的B点,D、E、F是OC连线上的点,OE=ED,DF=FC,OC连接上各点均可钉细钉子,每次均将摆球从A点由静止释放,不计绳与钉子碰撞时机械能的损失,不计空气阻力,下列说法正确的是( )| A. | 细线碰到钉子的前后瞬间,当球的线速度和角速度均增大 | |
| B. | 钉子钉在E点时,绳子最可能被拉断 | |
| C. | 若只在D点钉钉子,摆球最高只能摆到AB连线以下的某点 | |
| D. | 若只在F点以下某点钉钉子,摆球可能做完整的圆周运动 |
分析 细线碰到钉子的前后瞬间,球的线速度大小不变,根据半径的变化判断角速度的变化,结合牛顿第二定律分析钉子在哪一位置绳子拉力最大.绕半径较小,摆球可能做完整的圆周运动.
解答 解:A、细线碰到钉子的前后瞬间,球的线速度大小不变,转动的半径减小,根据$ω=\frac{v}{r}$知,角速度增大,故A错误.
B、根据牛顿第二定律得,F-mg=m$\frac{{v}^{2}}{r}$,解得F=mg+$m\frac{{v}^{2}}{r}$,钉子钉在E点时,相对于绕D、F点,转动的半径最大,拉力最小,绳子最不可能被拉断,故B错误.
C、由于绳与钉子碰撞时机械能的损失不计,若只在D点钉钉子,因D点与A等高,摆球最高能达到与A等高,故C错误.
D、若只在F点以下某点钉钉子,由于球做圆周运动的半径较小,摆球可能做完整的圆周运动,故D正确.
故选:D.
点评 解决本题的关键知道细线碰到钉子的前后瞬间,球的线速度大小不变,知道线速度与角速度的关系,以及知道小球最低点向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
13.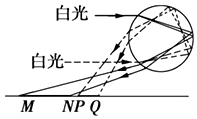 虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
 虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )
虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明.两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图8所示.关于照到M、N、P、Q点的单色光的说法中正确的是( )| A. | M、N、P、Q点的光的颜色分别为紫、红、红、紫 | |
| B. | M点的光的波动性较N点的光更显著 | |
| C. | 在同一单缝衍射装置上做实验,用P点的光得到的衍射图样的中央明纹宽度较Q点的光更窄 | |
| D. | 水中相同深度处有两个光源,其颜色分别与P、Q两点的光同色,在其正上方的水面之上,同等条件下观测,同P色的点光源在水下的像最深,且其照亮水面的面积最大 |
14.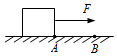 如图所示,静止在水平面上、质量为3kg的物体,在水平拉力F作用下从A点运动到B点的过程中,F对物体做功10J,摩擦力对物体做功-4J,则物体在B点时速度的大小为( )
如图所示,静止在水平面上、质量为3kg的物体,在水平拉力F作用下从A点运动到B点的过程中,F对物体做功10J,摩擦力对物体做功-4J,则物体在B点时速度的大小为( )
 如图所示,静止在水平面上、质量为3kg的物体,在水平拉力F作用下从A点运动到B点的过程中,F对物体做功10J,摩擦力对物体做功-4J,则物体在B点时速度的大小为( )
如图所示,静止在水平面上、质量为3kg的物体,在水平拉力F作用下从A点运动到B点的过程中,F对物体做功10J,摩擦力对物体做功-4J,则物体在B点时速度的大小为( )| A. | 2 m/s | B. | 4 m/s | C. | 6 m/s | D. | 10 m/s |
11. 在“探究加速度与力、质量的关系”实验中.某组同学实验得出数据,画出a-F图象如图所示,那么该组同学实验中出现的问题可能是( )
在“探究加速度与力、质量的关系”实验中.某组同学实验得出数据,画出a-F图象如图所示,那么该组同学实验中出现的问题可能是( )
 在“探究加速度与力、质量的关系”实验中.某组同学实验得出数据,画出a-F图象如图所示,那么该组同学实验中出现的问题可能是( )
在“探究加速度与力、质量的关系”实验中.某组同学实验得出数据,画出a-F图象如图所示,那么该组同学实验中出现的问题可能是( )| A. | 实验中摩擦力没有平衡 | |
| B. | 实验中摩擦力平衡过度 | |
| C. | 实验中绳子拉力方向没有跟平板平行 | |
| D. | 实验中小车质量发生变化 |
17. 如图所示,边长为L的正三角形区域内存在着垂直纸面向里的匀强磁场,质量为m、电荷量为q的带正电粒子以速率v从O点沿OB方向射入磁场,并从AB的中点C离开磁场,则磁场的磁感应强度的大小为( )
如图所示,边长为L的正三角形区域内存在着垂直纸面向里的匀强磁场,质量为m、电荷量为q的带正电粒子以速率v从O点沿OB方向射入磁场,并从AB的中点C离开磁场,则磁场的磁感应强度的大小为( )
 如图所示,边长为L的正三角形区域内存在着垂直纸面向里的匀强磁场,质量为m、电荷量为q的带正电粒子以速率v从O点沿OB方向射入磁场,并从AB的中点C离开磁场,则磁场的磁感应强度的大小为( )
如图所示,边长为L的正三角形区域内存在着垂直纸面向里的匀强磁场,质量为m、电荷量为q的带正电粒子以速率v从O点沿OB方向射入磁场,并从AB的中点C离开磁场,则磁场的磁感应强度的大小为( )| A. | $\frac{2\sqrt{3}mv}{3qL}$ | B. | $\frac{\sqrt{3}mv}{3qL}$ | C. | $\frac{\sqrt{3}mv}{2qL}$ | D. | $\frac{\sqrt{3}mv}{qL}$ |
4.甲、乙两人分别将同一桶水竖直向上匀速提升相同的高度,甲提水的速度比乙大,设甲、乙两人匀速提水过程中所做的功分别为 W甲和 W乙,做功的功率分别为 P甲和 P乙.下列关系正确的是( )
| A. | W甲>W乙 | B. | W甲<W乙 | C. | P甲>P乙 | D. | P甲<P乙 |
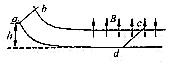 如图所示,宽为l、光滑的导电轨道的弧形部分处于磁场外,轨道的水平部分处于垂直轨道平面向上、磁感强度为B的匀强磁场中,质量为2m的金属杆cd静止在水平轨道上,另一质量为m的金属杆ab,从弧形轨道上h高处由静止开始下滑.设ab杆和cd杆始终与轨道垂直,且接触良好,ab杆与cd杆不会相碰,ab和cd杆的电阻均为R,轨道电阻不计.求:
如图所示,宽为l、光滑的导电轨道的弧形部分处于磁场外,轨道的水平部分处于垂直轨道平面向上、磁感强度为B的匀强磁场中,质量为2m的金属杆cd静止在水平轨道上,另一质量为m的金属杆ab,从弧形轨道上h高处由静止开始下滑.设ab杆和cd杆始终与轨道垂直,且接触良好,ab杆与cd杆不会相碰,ab和cd杆的电阻均为R,轨道电阻不计.求:


