题目内容
10.冰车上坐一人,总质量为M,冰面上还有一个质量为m的弹性滑块,都处于静止状态,某一时刻坐在冰车上的人用力将滑块推向前方一个固定挡板,若此时滑块相对冰面的速度为v0,滑块碰撞后沿原线返回,滑块与固定挡板的碰撞时弹性碰撞,反弹回来的滑块被冰车上的人再一次推向前方的固定挡板,保持滑块对冰面的速度v0不变,如此反复多次,已知M=16m,求:(1)滑块第一次被推出时,冰车的速度是多大?
(2)人推出滑块多少次后将不可能再接到滑块?
分析 (1)对滑块与冰车进行研究由动量守恒定律可求得冰车的速度;
(2)将人、冰车及滑块作为整体,由动量定理可求得人动量的改变量;当冰车的速度大于v0时将不能再接到滑块;则可求得推出的次数.
解答 解:(1)设滑块的速度为正方向;由动量守恒定律可知:
mv0+Mv=0
解得:v=-$\frac{m{v}_{0}}{M}$=-$\frac{{v}_{0}}{16}$;
负号说明冰车与滑块的速度方向相反.
(2)将人、冰车与滑块作为整体.挡板每次对滑块的冲量I0=2mv0,对系统来说,这个冲量即外力的冲量,即人每推滑块一次,挡板对所研究的整体一个冲量I0=2mv0.设人推n次后,冰车的速度为v,对整体应用动量定理ΣI0=△P
即n(2mv0)=mv0+Mv;人不能再接到滑块应有:v≥v0
可解得n≥$\frac{1}{2}$($\frac{M}{m}$+1)=$\frac{1}{2}(16+1)$=8.25;
应取n=9.
答:(1)冰车的速度为$\frac{{v}_{0}}{16}$;
(2)人推出滑块9次后不能再接到滑块.
点评 本题考查动量守恒定律及动量定理,要注意正确选择研究对象,明确应用动量守恒及动量定理进行分析求解.

练习册系列答案
相关题目
20.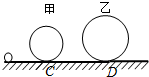 在水平地面上,有如图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通.让一小球以一定的初速先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道.下列说法正确的是( )
在水平地面上,有如图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通.让一小球以一定的初速先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道.下列说法正确的是( )
 在水平地面上,有如图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通.让一小球以一定的初速先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道.下列说法正确的是( )
在水平地面上,有如图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通.让一小球以一定的初速先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道.下列说法正确的是( )| A. | 小球最后离开两圆轨道时的速度小于滑上甲轨道时的初速度 | |
| B. | 小球经过甲轨道最高点时比经过乙轨道最高点时速度大 | |
| C. | 小球经过甲、乙轨道最低点时对轨道的压力相等 | |
| D. | 小球经过甲、乙轨道最高点时对轨道的压力相等 |
1. 如图所示的倾斜木板,在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在1号球的右侧有一光滑竖直挡板,若缓慢转动挡板至与斜面垂直,则在此过程中( )
如图所示的倾斜木板,在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在1号球的右侧有一光滑竖直挡板,若缓慢转动挡板至与斜面垂直,则在此过程中( )
 如图所示的倾斜木板,在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在1号球的右侧有一光滑竖直挡板,若缓慢转动挡板至与斜面垂直,则在此过程中( )
如图所示的倾斜木板,在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在1号球的右侧有一光滑竖直挡板,若缓慢转动挡板至与斜面垂直,则在此过程中( )| A. | 1、2两球间的弹力不变 | B. | 1球对挡板的压力逐渐减小 | ||
| C. | 1球对斜面的压力逐渐增大 | D. | 5、6两球间的弹力不变 |
15.伽利略在《两种新科学的对话》中写道:“假设你在密闭的船舱里,在你跳跃时,你将和以前一样,在船底板上跳过相同的距离,你跳向船尾也不会比跳向船头来的远.你把不论什么东西扔给你的同伴时,不论他是在船头还是在船尾,只要你自己站在对面,你也并不需要用更多的力,水滴将垂直滴进下面的罐子,一滴也不会滴向船尾.”如果上述现象能够实现,该船的运动形式可能为( )
| A. | 匀速直线运动 | B. | 匀加速直线运动 | C. | 匀减速直线运动 | D. | 静止 |
8.如图所示“用DIS研究机械能守恒定律”实验装置.下列步骤正确的是( )


| A. | 让摆锤自然下垂,调整标尺盘,使其竖直线与摆锤线平行 | |
| B. | 将摆锤置于释放器内,释放杆进行伸缩调整,使摆锤的系线松弛一点便于摆锤释放 | |
| C. | 调整光电门的位置,使光电门的接收孔与测量点位于同一水平面内 | |
| D. | 将释放器先后置于A、B、C点,将光电门置于标尺盘的D点,分别测量释放器内的摆锤由A、B、C三点静止释放摆到D点的势能和动能 |
 质量为0.1kg 的弹性球从空中某高度由静止开始下落经0.5s落至地面,该下落过程对应的v-t图象如图所示.球与水平地面相碰后离开地面时的速度大小为碰撞前的$\frac{1}{2}$.设球受到的空气阻力大小恒为f,取g=10m/s2,求:
质量为0.1kg 的弹性球从空中某高度由静止开始下落经0.5s落至地面,该下落过程对应的v-t图象如图所示.球与水平地面相碰后离开地面时的速度大小为碰撞前的$\frac{1}{2}$.设球受到的空气阻力大小恒为f,取g=10m/s2,求:
 已知试验中所用的滑动变阻器阻值范围为0~10Ω,电流表内阻约几欧,电压表内阻约20kΩ,电源为干电池,电源电动势E=4.5V,内阻较小,则以下电路图中,A(选填字母代表)电路为本次实验应当采用的最佳电路,但用此最佳电路测量的金属丝电阻仍然会比真实值偏偏小(选填“大”或“小”).误差是因为电压表分流引起的.
已知试验中所用的滑动变阻器阻值范围为0~10Ω,电流表内阻约几欧,电压表内阻约20kΩ,电源为干电池,电源电动势E=4.5V,内阻较小,则以下电路图中,A(选填字母代表)电路为本次实验应当采用的最佳电路,但用此最佳电路测量的金属丝电阻仍然会比真实值偏偏小(选填“大”或“小”).误差是因为电压表分流引起的. 某同学想利用滑块在倾斜气垫导轨上的运动来验证动能定理,如图所示,测量步骤如下:
某同学想利用滑块在倾斜气垫导轨上的运动来验证动能定理,如图所示,测量步骤如下: