题目内容
4.如图所示,水平轨道左端与长L=1.25m的水平传送带相接,传送带逆时针匀速运动的速度v0=1m/s.轻弹簧右端固定在光滑水平轨道上,弹簧处于自然状态.现用质量m=0.1kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9kg的长木板上.竖直半圆轨道的半径R=0.4,物块与传送带间动摩擦因数μ1=0.8,物块与木板间动摩擦因数μ2=0.25,取g=10m/s2.求:
(1)物块到达B点时速度vB的大小.
(2)弹簧被压缩时的弹性势能EP.
(3)若长木板与水平地面间动摩擦因数μ3≤0.026时,要使小物块恰好不会从长木板上掉下,木板长度S的范围是多少 (设最大静动摩擦力等于滑动摩擦力).
分析 (1)据恰好做圆周运动,利用牛顿运动定律列方程求解.
(2)抓住物块在B点的速度大于传送带的速度,可知物块在传送带上一直做匀减速运动,根据动能定理求出A点的速度,结合能量守恒定律求出弹簧的弹性势能.
(3)根据机械能守恒定律求出C点的速度,讨论μ3=0,μ3=0.026时,通过动量守恒定律和功能关系,以及动能定理求出木板的长度,从而得出木板的范围.
解答 解:(1)物体在光滑半圆轨道最高点恰好做圆周运动,由牛顿第二定律得:$mg=m\frac{{{v}_{B}}^{2}}{R}$ ①
解得${v}_{B}=\sqrt{gR}=\sqrt{10×0.4}m/s=2m/s$.②
(2)物块被弹簧弹出的过程中,物块和弹簧组成的系统机械能守恒:${E}_{p}=\frac{1}{2}m{{v}_{A}}^{2}$ ③
vB>v0=1m/s,物体在传送带上一直做匀减速运动.
物块在传送带上滑行过程由动能定理得:-f1L=$\frac{1}{2}m{{v}_{B}}^{2}-\frac{1}{2}m{{v}_{A}}^{2}$ ④
f1=μ1mg=0.8N ⑤
联立②③④⑤解得:Ep=1.2J ⑥
(3)物块从B到C过程中由机械能守恒定律得:$mg2R=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{B}}^{2}$,⑦
联立②⑥解得:${v}_{C}=2\sqrt{5}$m/s ⑧
讨论:Ⅰ.当μ3=0时,小物块恰好不会从长木板上掉下长度为s1,
小物块和长木板共速为v,由动量守恒定律:mvC=(M+m)v ⑨
由功能关系:${μ}_{2}mg{s}_{1}=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}(M+m){v}^{2}$ ⑩
代入数据解得s1=3.6m(11)
Ⅱ.当μ3=0.026时,小物块恰好不会从长木板上掉下长度为s2,
物块在长木板上滑行过程中,对长木板受力分析:
上表面受到的摩擦力f2=μ2mg=0.25×1N=0.25N.(12)
下表面受到的摩擦力f3≤μ3(M+m)g=0.026×10N=0.26N
所以长木板静止不动,对物块在长木板上滑行过程
由动能定理得:-${f}_{2}{s}_{2}=0-\frac{1}{2}m{{v}_{C}}^{2}$ (13)
代入数据解得s2=4m(14)
所以木板长度的范围是3.6m≤s≤4m(15)
答:(1)物块到达B点时速度vB的大小为2m/s.
(2)弹簧被压缩时的弹性势能为1.2J.
(3)要使小物块恰好不会从长木板上掉下,木板长度S的范围是3.6m≤s≤4m.
点评 分析清楚滑块的运动情况和受力情况是解题的关键,据受力情况判断滑块的运动是解题的核心,灵活利用牛顿运动定律、动能定理和能量守恒定律,动量守恒定律进行求解.

 如图所示,在竖直向上的匀强电场中,A球位于B球的正上方,质量相等的两个小球以相同初速度水平抛出,它们最后落在水平面上同一点,其中只有一个小球带电,不计空气阻力,下例判断正确的是( )
如图所示,在竖直向上的匀强电场中,A球位于B球的正上方,质量相等的两个小球以相同初速度水平抛出,它们最后落在水平面上同一点,其中只有一个小球带电,不计空气阻力,下例判断正确的是( )| A. | 如果A球带电,则A球一定带负电 | |
| B. | 如果A球带电,则A球的电势能一定增加 | |
| C. | 如果B球带电,则B球一定带负电 | |
| D. | 如果B球带电,则B球的电势能一定增加 |
 2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则( )
2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则( )| A. | 卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度小 | |
| B. | 卫星在轨道Ⅲ上经过P点的速度比在轨道Ⅰ上经过P点时大 | |
| C. | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短 | |
| D. | 卫星在轨道Ⅰ上经过P点比在轨道Ⅱ上经过P点时的速度大 |

| A. | 等于0 | B. | 等于F | C. | 大于F | D. | 小于F |
| A. | 太阳帆板展开的位置 | B. | 月球表面上的着陆点 | ||
| C. | 环月椭圆轨道的近月点 | D. | 环月椭圆轨道的远月点 |
 利用发波水槽得到的水面波形如a、b所示,则图a显示了波的衍射现象.为了能更明显看到此现象,可以减小水波的振源频率(选填“增大”、“减小”).
利用发波水槽得到的水面波形如a、b所示,则图a显示了波的衍射现象.为了能更明显看到此现象,可以减小水波的振源频率(选填“增大”、“减小”). 如图所示,一根左侧弯成$\frac{1}{4}$圆弧的光滑细管固定在竖直平面内,圆弧半径R=0.5m,水平部分足够长.初始时,一根质量m=1kg、与管道$\frac{1}{4}$圆弧部分等长的柔软匀质绳在水平拉力F0作用下静止在管道中.现将绳子全部缓慢拉入水平管道内,需要拉力F0做功W=1.82J.g取10m/s2,π取3.14.求:
如图所示,一根左侧弯成$\frac{1}{4}$圆弧的光滑细管固定在竖直平面内,圆弧半径R=0.5m,水平部分足够长.初始时,一根质量m=1kg、与管道$\frac{1}{4}$圆弧部分等长的柔软匀质绳在水平拉力F0作用下静止在管道中.现将绳子全部缓慢拉入水平管道内,需要拉力F0做功W=1.82J.g取10m/s2,π取3.14.求: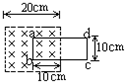 单匝矩形线圈abcd部分地放置在具有理想边界的匀强磁场中,磁感应强度为0.1T,线圈绕ab轴以100p rad/s角速度匀速旋转,如图所示,当线圈由图示位置转过60°,在这过程中感应电动势平均值为多大?当转过90°时,感应电动势即时值为多大?
单匝矩形线圈abcd部分地放置在具有理想边界的匀强磁场中,磁感应强度为0.1T,线圈绕ab轴以100p rad/s角速度匀速旋转,如图所示,当线圈由图示位置转过60°,在这过程中感应电动势平均值为多大?当转过90°时,感应电动势即时值为多大?