题目内容
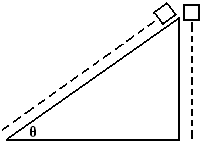 (2005?上海模拟)如图所示,物体从倾角为θ的斜面顶端由静止沿斜面滑下,它滑到底端的速度是它从同样高度自由下落的速度的k倍(k<1),则物体沿斜面下滑时间t1与自由落体时间t2之比为多少,物体与斜面的摩擦系数为多大.
(2005?上海模拟)如图所示,物体从倾角为θ的斜面顶端由静止沿斜面滑下,它滑到底端的速度是它从同样高度自由下落的速度的k倍(k<1),则物体沿斜面下滑时间t1与自由落体时间t2之比为多少,物体与斜面的摩擦系数为多大.分析:设斜面长为l,高为h.根据匀变速运动的位移x=
,结合物体沿斜面运动与自由落体运动时间关系,联立可求得时间之比;
根据动能定理列式求解物体与斜面的摩擦系数.
| v0+v |
| 2 |
根据动能定理列式求解物体与斜面的摩擦系数.
解答:解:设斜面长为l,高为h.有h=lsinθ,则
l=
t1,h=
t2
已知:
=k,故有
=
=
根据动能定理:mgh-μmgcosθ?l=
m
,mgh=
m
两式相比:1-
=
=k2,
解得:μ=(1-k2)tgθ
答:物体沿斜面下滑时间t1与自由落体时间t2之比为1:ksinθ,物体与斜面的摩擦系数为(1-k2)tgθ.
l=
| v1 |
| 2 |
| v2 |
| 2 |
已知:
| v1 |
| v2 |
| t1 |
| t2 |
| l?v2 |
| h?v1 |
| 1 |
| ksinθ |
根据动能定理:mgh-μmgcosθ?l=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
两式相比:1-
| μlcosθ |
| h |
| ||
|
解得:μ=(1-k2)tgθ
答:物体沿斜面下滑时间t1与自由落体时间t2之比为1:ksinθ,物体与斜面的摩擦系数为(1-k2)tgθ.
点评:本题关键是掌握匀变速运动的位移公式x=
和动能定理,并正确运用.
| v0+v |
| 2 |

练习册系列答案
相关题目
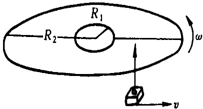 (2005?上海模拟)一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是
(2005?上海模拟)一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是 (2005?上海模拟)用如图所示的传统打气筒给容器打气,设打气筒的容积为V0,底部有一阀门K可自动开启并不漏气,活塞A上提时外界大气可从其四周进入打气筒,活塞下移时可把打气筒内气体推入B中.若B的容积为4V0,A、B内气体初始压强等于大气压P0,为使B中气体压强达到10P0,则需打气
(2005?上海模拟)用如图所示的传统打气筒给容器打气,设打气筒的容积为V0,底部有一阀门K可自动开启并不漏气,活塞A上提时外界大气可从其四周进入打气筒,活塞下移时可把打气筒内气体推入B中.若B的容积为4V0,A、B内气体初始压强等于大气压P0,为使B中气体压强达到10P0,则需打气 (2005?上海模拟)如图所示,硬杆一端铰链固定在墙上的B点,另一端装有滑轮,重物用绳拴住通过滑轮固定于墙上的A点,若杆、滑轮及绳的质量和摩擦均不计,将绳的固定端从A点稍向下移,再使之平衡时,则( )
(2005?上海模拟)如图所示,硬杆一端铰链固定在墙上的B点,另一端装有滑轮,重物用绳拴住通过滑轮固定于墙上的A点,若杆、滑轮及绳的质量和摩擦均不计,将绳的固定端从A点稍向下移,再使之平衡时,则( )