题目内容
14. 如图所示,光滑水平面上有一左端靠墙的长板车,车的上表面BC段是水平轨道,水平轨道左侧是固定在车上的一光滑斜面轨道,斜面轨道与水平轨道在B点平滑连接.C点的右侧光滑,长板车的右端固定一个处于原长状态的轻弹簧,弹簧自由端恰在C点.质量m=1kg的物块(视为质点)从斜面上A点由静止滑下,A、B间的高度h=1.8 m,经AB和BC段后压缩弹簧,弹簧弹性势能的最大值Ep=3J.斜面和长板车的总质量M=2kg.物块与长板车的水平轨道间的动摩擦因数μ=0.3,g取10m/s2,求:
如图所示,光滑水平面上有一左端靠墙的长板车,车的上表面BC段是水平轨道,水平轨道左侧是固定在车上的一光滑斜面轨道,斜面轨道与水平轨道在B点平滑连接.C点的右侧光滑,长板车的右端固定一个处于原长状态的轻弹簧,弹簧自由端恰在C点.质量m=1kg的物块(视为质点)从斜面上A点由静止滑下,A、B间的高度h=1.8 m,经AB和BC段后压缩弹簧,弹簧弹性势能的最大值Ep=3J.斜面和长板车的总质量M=2kg.物块与长板车的水平轨道间的动摩擦因数μ=0.3,g取10m/s2,求:①车的上表面BC段的长度;
②物块向右压缩弹簧的过程中,弹簧对物块的冲量大小.
分析 ①对下滑过程由机械能守恒定律可得物块到达B点的速度,再根据动量守恒定律可功能关系列式,联立即可求得BC段的长度;
②对BC过程根据动量守恒定律和功能关系可求得C点的速度,再由动量定理即可求得弹簧对物块的冲量大小.
解答 解:①下滑过程中,对物块有:
mgh=$\frac{1}{2}$mv02-0
物块滑下后,当两者第一次等速时,弹簧的弹性势能最大,由动量守恒定律和功能关系可知:
mv0=(m+M)v'
μmgL+EP=$\frac{1}{2}$mv02-$\frac{1}{2}$(M+m)v'2
解得:v'=4m/s;
L=3m.
②物块从B点运动到C点的过程中,有:
mv0=mv1+Mv2
-μmgL=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22-$\frac{1}{2}$mv02
解得:v1=4m/s
由动量定理有:
I=mv'-mv1
解得:I=-2N•s,
所求冲量大小为2Ns.
答:①车的上表面BC段的长度为3m;
②物块向右压缩弹簧的过程中,弹簧对物块的冲量大小2N•s.
点评 本题考查了求速度、弹性势能、距离问题,本题难度较大,分析清楚物体的运动过程是正确解题的关键,要注意明确系统不受外力,总动量守恒,但在分析能量时要注意应包含弹簧的弹性势能.

练习册系列答案
相关题目
5. 如图所示,虚线a,b,c,d表示匀强电场中的4个等势面,两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.己知M是带正电的带电粒子.则( )
如图所示,虚线a,b,c,d表示匀强电场中的4个等势面,两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.己知M是带正电的带电粒子.则( )
 如图所示,虚线a,b,c,d表示匀强电场中的4个等势面,两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.己知M是带正电的带电粒子.则( )
如图所示,虚线a,b,c,d表示匀强电场中的4个等势面,两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.己知M是带正电的带电粒子.则( )| A. | N一定也带正电 | B. | a点的电势高于b点的电势 | ||
| C. | 带电粒子N克服电场力做功 | D. | 带电粒子N的动能增大,电势能减小 |
2. 如图所示是一沿笔直公路做匀加速直线运动的汽车的速度计.某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图(甲)所示的位置,经过7s后指针位置如图(乙)所示.有关上述运动过程,下列说法中正确的是( )
如图所示是一沿笔直公路做匀加速直线运动的汽车的速度计.某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图(甲)所示的位置,经过7s后指针位置如图(乙)所示.有关上述运动过程,下列说法中正确的是( )
 如图所示是一沿笔直公路做匀加速直线运动的汽车的速度计.某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图(甲)所示的位置,经过7s后指针位置如图(乙)所示.有关上述运动过程,下列说法中正确的是( )
如图所示是一沿笔直公路做匀加速直线运动的汽车的速度计.某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图(甲)所示的位置,经过7s后指针位置如图(乙)所示.有关上述运动过程,下列说法中正确的是( )| A. | 由图直接读出的是汽车运动的平均速度 | |
| B. | 乙图直接读出的是汽车运动7s时的瞬时速率 | |
| C. | 汽车运动的加速度约为5.7 m/s2 | |
| D. | 汽车运动的加速度约为1.6 m/s2 |
6.一物体从斜面顶端由静止开始匀加速滑下,到达斜面中点用时1s,速度为2m/s,则下列说法正确的是( )
| A. | 物体运动的加速度为1m/s2 | B. | 斜面长度为2m | ||
| C. | 物体在斜面上运动的总时间为2s | D. | 物体到达斜面底端时的速度为4m/s |
3.如图为一列横波的波形图,该波的波长为( )


| A. | 4cm | B. | 8cm | C. | 20cm | D. | 40cm |
4.如图为点电荷Q的电场中的三条电场线,下面说法正确的是( )


| A. | 若Q为负电荷,EA<EB | B. | 若Q为负电荷,EA>EB | ||
| C. | 若Q为正电荷,EA<EB | D. | 若Q为正电荷,EA>EB |

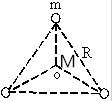 据探测,宇宙中可能存在一种远离其他恒星的四星系统,其中有一种四星系统的模型如图所示,在边长为R的正三角形的三个顶点上各有一质量为m的星体,在三角形的中心有质量为M的另一颗星,处在三角形顶点上的三颗星均绕处于静止状态的位于三角形中心的星体做匀速圆周运动,不考虑其他星体对该系统的影响,已知引力常量为G,求三角形顶点上的星体做匀速圆周运动的周期和线速度.
据探测,宇宙中可能存在一种远离其他恒星的四星系统,其中有一种四星系统的模型如图所示,在边长为R的正三角形的三个顶点上各有一质量为m的星体,在三角形的中心有质量为M的另一颗星,处在三角形顶点上的三颗星均绕处于静止状态的位于三角形中心的星体做匀速圆周运动,不考虑其他星体对该系统的影响,已知引力常量为G,求三角形顶点上的星体做匀速圆周运动的周期和线速度. 如图所示,在足够长的水平台面上静置一质量为1kg的长木板A,左端用足够长的轻绳绕过光滑定滑轮与固定在地面上的电动机相连.电动机先以恒定的拉力向左拉动木板A,当木板运动了0.2m时速度达到2m/s,此时电动机达到最大输出功率.与此同时,将相对于地面静止的小物块B轻放在木版A的最左端,小物块B质量也为1kg,此后电动机保持输出功率不变,经过时间t=2s,B与A达到共速.已知A与桌面间的动摩擦因数为μ1=0.20,A、B间的动摩擦因数μ2=0.20,重力加速度g取10m/s2.求:
如图所示,在足够长的水平台面上静置一质量为1kg的长木板A,左端用足够长的轻绳绕过光滑定滑轮与固定在地面上的电动机相连.电动机先以恒定的拉力向左拉动木板A,当木板运动了0.2m时速度达到2m/s,此时电动机达到最大输出功率.与此同时,将相对于地面静止的小物块B轻放在木版A的最左端,小物块B质量也为1kg,此后电动机保持输出功率不变,经过时间t=2s,B与A达到共速.已知A与桌面间的动摩擦因数为μ1=0.20,A、B间的动摩擦因数μ2=0.20,重力加速度g取10m/s2.求: