题目内容
如图所示，PQ是两块平行金属板，上极板接电源正极，两极板之间的电压为U =1.2×104V，一群带负电粒子不停的通过P极板的小孔以速度v0=2.0×104m/s垂直金属板飞入，通过Q极板上的小孔后，垂直AC边的中点O进入边界为等腰直角三角形的匀强磁场中，磁感应强度为B=1.0T，边界AC的长度为a=1.6m，粒子比荷
．不计粒子的重力．求：
（1）粒子进入磁场时的速度大小是多少？
（2）粒子在磁场中运动的时间？打在什么位置？
（3）若在两极板间加一正弦交变电压U =9.6×104sin314t（V），则这群粒子可能从磁场边界的哪些区域飞出？并求出这些区域．（每个粒子在电场中运动时，可认为电压是不变的）
解：（1）粒子从P极板进入电场后，做加速运动，有：
…………………………（2分）
…………………………（1分）
（2）粒子在磁场中做匀速圆周运动，有：
…………………………（1分）
…………………………（1分）
垂直地打在BC边的中点。 ……………………（1分）
粒子在磁场中运动的周期为
…………………………（1分）
偏转角为90°， …………………………（1分）
…………………………（1分）
（3）当粒子以反向最大电压进入电场时，粒子不能穿过Q点进入磁场。……（1分）
t=0时刻射入的粒子，没有经过加速，粒子将以v0=2.0×104m/s从O点射入磁场，
。恰好打到C点 …………（1分）
因此OC边可以全部打到。
当粒子以正向最大电压加速进入电场中，
最大速度
m/s …………………………（1分）
………………（1分）
若粒子与AB边相切飞出，如图所示，根据几何关系可得：
BF+FC=a，R切=PF+FO1，可得：
…………（1分）
由以上三个半径关系可知，粒子从BC 和AB边飞出。 ………………（1分）
若恰好与AB相切的粒子打在BC边E离C点的距离为：
m
在EC之间均有粒子飞出 ……（1分）
与AB边相切的切点P到B点的距离为：
m ……（1分）
当粒子以最大速度进入磁场时，粒子将从AB边界的G点飞出，设OD之间的距离为x，则：
GD=AD=x+a/2，DO2=Rmax-x，根据几何关系可得：
可得x=0.4m
最大速度粒子从AB边上射出点G到B点的距离为：0.4
m
在GP之间均有粒子飞出 …………（1分）
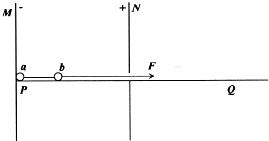如图所示，MN是两块竖直放置的带电平行板，板内有水平向左的匀强电场，PQ是光滑绝缘的水平滑槽，滑槽从N板中间穿入电场．a、b为两个带等量正电荷的相同小球，两球之间用绝缘水平轻杆固连，轻杆长为两板间距的
（2013?宁波二模）如图所示，PQ是两块平行金属板，上极板接电源正极，两极板之间的电压为U=1.2×104V，一群带负电粒子不停的通过P极板的小孔以速度v0=2.0×104m/s垂直金属板飞入，通过Q极板上的小孔后，垂直AC边的中点O进入边界为等腰直角三角形的匀强磁场中，磁感应强度为B=1.0T，边界AC的长度为a=1.6m，粒子比荷
，杆长远大于球的半径，开始时从外面用绝缘轻绳拉着b球使a球靠近M板但不接触。现对轻绳施以沿杆方向的水平恒力拉着b球和a球由静止向右运动，当b球刚从小孔离开电场时，撤去拉力，之后a球也恰好能离开电场。求运动过程中b球离开电场前和离开电场后（a球还在电场中）轻杆中的弹力之比。不计两球间库仑力，球视为点电荷。
。不计粒子的重力。