题目内容
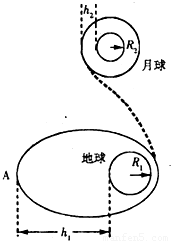
如图所示，“嫦娥奔月”的过程可以简化为：“嫦娥一号”升空后，绕地球沿椭圆轨道运动，远地点A距地面高度为h1，然后经过变轨被月球捕获，再经多次变轨，最终在距离月球表面高度为h2的轨道上绕月球做匀速圆周运动．若已知地球的半径为R1、表面重力加速度为g1；月球的质量为M2，半径为R2，引力常量为G，根据以上信息，不可以确定的是（ ）
| A．“嫦娥一号”在远地点A时的速度 |
| B．“嫦娥一号”在远地点A时的加速度 |
| C．“嫦娥一号”绕月球运动的周期 |
| D．月球表面的重力加速度 |
A、根据牛顿第二定律得
“嫦娥一号”在远地点A时万有引力等于其合力．
=ma①
忽略地球自转的影响，根据万有引力等于重力列出等式．
=m′g1 ②
由①②可求得“嫦娥一号”在远地点A时的加速度．
由于轨道是椭圆，在远地点A时的速度无法确定，故A错误，B正确．
C、“嫦娥一号”绕月球运动根据万有引力提供向心力，列出等式
=m（R1+h2）
③
忽略月球自转的影响，根据万有引力等于重力列出等式
=m′g2④
由③④可求得“嫦娥一号”绕月球运动的周期和月球表面的重力加速度，故C、D正确．
本题选错误的，故选A．
“嫦娥一号”在远地点A时万有引力等于其合力．
| GMm |
| (R1+h1)2 |
忽略地球自转的影响，根据万有引力等于重力列出等式．
| GMm′ |
| R12 |
由①②可求得“嫦娥一号”在远地点A时的加速度．
由于轨道是椭圆，在远地点A时的速度无法确定，故A错误，B正确．
C、“嫦娥一号”绕月球运动根据万有引力提供向心力，列出等式
| GM2m |
| (R2+h2)2 |
| 4π2 |
| T2 |
忽略月球自转的影响，根据万有引力等于重力列出等式
| GM2m′ |
| R22 |
由③④可求得“嫦娥一号”绕月球运动的周期和月球表面的重力加速度，故C、D正确．
本题选错误的，故选A．
练习册系列答案
相关题目
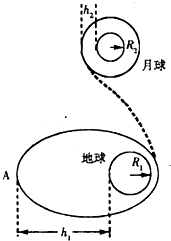如图所示，“嫦娥奔月”的过程可以简化为：“嫦娥一号”升空后，绕地球沿椭圆轨道运动，远地点A距地面高度为h1，然后经过变轨被月球捕获，再经多次变轨，最终在距离月球表面高度为h2的轨道上绕月球做匀速圆周运动．若已知地球的半径为R1、表面重力加速度为g1；月球的质量为M2，半径为R2，引力常量为G，根据以上信息，不可以确定的是（ ）
距离月球表面高为h2的轨道上绕月球做匀速圆周运动。若已知地球的半径为R1、表面重力加速度为g0，月球的质量为M、半径为R2，引力常量为G，根据以上信息，可以确定（ ） 
如图所示，“嫦娥奔月”的过程可以简化为：“嫦娥一号”升空后，绕地球沿椭圆轨道运动，远地点A距地面高为h1，然后经过变轨被月球捕获，再经多次变轨，最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动。若已知地球的半径为R1、表面重力加速度为g0，月球的质量为M、半径为R2，引力常量为G，根据以上信息，可以确定（ ）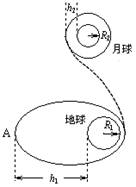 
如图所示，“嫦娥奔月”的过程可以简化为：“嫦娥一号”升空后，绕地球沿椭圆轨道运动，远地点A距地面高为h1，然后经过变轨被月球捕获，再经多次变轨，最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动。若已知地球的半径为R1、表面重力加速度为g0，月球的质量为M、半径为R2，引力常量为G，根据以上信息，可以确定（ ）
