Question

如图甲所示的控制电子运动装置由偏转电场、偏转磁场组成．偏转电场处在加有电压U、相距为d的两块水平平行放置的导体板之间，匀强磁场水平宽度一定，竖直长度足够大，其紧靠偏转电场的右边．大量电子以相同初速度连续不断地沿两板正中间虚线的方向向右射入导体板之间．当两板间没有加电压时，这些电子通过两板之间的时间为2t₀；当两板间加上图乙所示的电压U时，所有电子均能通过电场、穿过磁场，最后打在竖直放置的荧光屏上．已知电子的质量为m、电荷量为e，不计电子的重力及电子间的相互作用，电压U的最大值为U₀，磁场的磁感应强度大小为B、方向水平且垂直纸面向里．
（1）如果电子在t=t₀时刻进入两板间，求它离开偏转电场时竖直分位移的大小．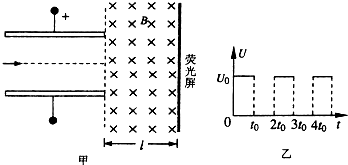
（2）要使电子在t=0时刻进入电场并能最终垂直打在荧光屏上，匀强磁场的水平宽度l为多少？
（3）在满足第（2）问的情况下，打在荧光屏上的电子束的宽度为多少？

Answer 1

分析：没有电场时电子在平行板间匀速直线运动，有电场时电子做类平抛运动，根据几何关系求解．

解答：解：（1）电子在t=t₀时刻进入两板间，先做匀速运动，后做类平抛运动
在2t₀～3t₀时间内发生偏转y=

1

2

a

t

2 0

=

1

2

eE

m

t

2 0

=

1

2

×

eU0

md

×

t

2 0

=

eU0 t 2 0

2md

（2）设电子从电场中射出的偏向角为θ，速度为v，如图所示：

则：
vy=at0=

eU0t0

md

sinθ=

vy

v

=

eU0t0

mdv

电子通过匀强磁场并能垂直打在荧光屏上，设其圆周运动的半径为R
根据牛顿第二定律有evB=m

v2

R

根据几何关系得：sinθ=

l

R

得水平宽度l=

U0t0

Bd

（3）由题意可知，要使电子的侧向位移最大，应让电子从0、2t₀、4t_o…等时刻进入偏转电场，在这种情况下，电子的偏向位移为
ymax=

1

2

a

t

2 0

+vyt0=

1

2

×

eU0

md

×

t

2 0

+

eU0

md

t

2 0

要使电子的侧向位移最小，应让电子从t₀、3t_o…等时刻进入偏转电场，在这种情况下，电子的侧向位移为mdymin=

1

2

a

t

2 0

=

1

2

×

eU0

md

t

2 0

所以电子从偏转电场中出来时的最大侧向位移和最小侧向位移的差值为：
△y=y_max-y_min=

eU0

md

t

2 0

因进入偏转磁场时电子速度大小v=

v 2 0 + v 2 y

相同，方向平行，所以电子在磁场中的轨道半径相同，都垂直打在荧光屏上，所以打在荧光屏上的电子束宽度为
△y=

eU0

md

t

2 0

答：（1）如果电子在t=t₀时刻进入两板间，求它离开偏转电场时竖直分位移的大小为

eU0 t 2 0

2md

．
（2）要使电子在t=0时刻进入电场并能最终垂直打在荧光屏上，匀强磁场的水平宽度l为l=

U0t0

Bd

；
（3）在满足第（2）问的情况下，打在荧光屏上的电子束的宽度为

eU0

md

t

2 0

．

点评：会用运动的合成与分解处理类平抛运动问题，根据物体运动的受力情况，确定粒子运动性质，确定物体运动的轨迹并能根据几何关系求解．