题目内容
（2008?邵阳模拟）如图所示，物体M与m紧靠着置于动摩擦因数为μ的斜面上，斜面的倾角为θ，现施一水平力F作用于M，M和m共同向上加速运动，求它们之间相互作用力的大小．分析：先用整体法列出牛顿第二定律，由此得到加速度的表达式，进而用隔离法单独对m受力分析，列牛顿第二定律，可以解得两者之间的相互作用．
解答：解析：两个物体具有共同的沿斜面向上的加速度，所以可以把它们作为一个整体，其受力如图16所示，建立图示坐标系，
F1=（M+m）gcosθ+Fsinθ… ①
由牛顿第二定律得：
Fcosθ-F2-（M+m）gsinθ=（M+m）a…②
且F2=μF1 …③
为求两个物体之间的相互作用力，把两物体隔离开，对m受力分析如图17所示，由牛顿第二定律得：
F1′-mgcosθ=0… ④
FN-F2′-mgsinθ=ma… ⑤
且F2′=μF1′…⑥
联立①～⑥式可得：
FN=
答：它们之间相互作用力的大小为FN=
F1=（M+m）gcosθ+Fsinθ… ①
由牛顿第二定律得：
Fcosθ-F2-（M+m）gsinθ=（M+m）a…②
且F2=μF1 …③
为求两个物体之间的相互作用力，把两物体隔离开，对m受力分析如图17所示，由牛顿第二定律得：
F1′-mgcosθ=0… ④FN-F2′-mgsinθ=ma… ⑤
且F2′=μF1′…⑥
联立①～⑥式可得：
FN=
| mF(cosθ-μsinθ) |
| M+m |
答：它们之间相互作用力的大小为FN=
| mF(cosθ-μsinθ) |
| M+m |
点评：本题是斜面上的连接体问题，主要考查牛顿第二定律和动摩擦力知识的应用，整体法与隔离法的结合应用是解答本题的切入点．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
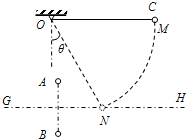（2008?邵阳模拟）如图所示，在同一条竖直线上，有电荷量均为Q的A、B两个正点电荷，； GH是它们连线的垂直平分线．另有一个带电小球C，质量为m、电荷量为+q（可视为点电荷），被长为L的绝缘轻细线悬挂于O点，现在把小球C拉起到M点，使细线水平且与 A、B处于同一竖直面内，由静止开始释放，小球C向下运动到GH线上的N点时刚好速度为零，此时细线与竖直方向的夹角θ=30°．试求：
（2008?邵阳模拟）如图所示，物块P静止在水平放置的固定木板上，若分别对P施加相互垂直的两个水平拉力F1和F2作用时（F1＞F2），P将分别沿F1和F2的方向匀加速滑动，其受到的滑动摩擦力木小分别为f1和f2，其加速度大小分别为a1和a2；若从静止开始同时对P施加上述二力，其受到的滑动摩擦力大小为f3，其加速度大小为a3，关于以上各物理量之间的关系，判断正确的是（ ）