题目内容
如图所示光滑水平直轨道上有三个滑块A、B、C质量分别为mA=mC=2m和mB=m，A、B用细绳相连，中间有一压缩的弹簧（弹簧与滑块不栓接），开始时A、B以共同速度V向右运动，C静止，某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三者的速度恰好相同．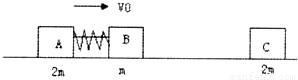
求：（1）B与C碰撞前B的速度
（2）弹簧释放的弹性势能多大．
【答案】分析：（1）A、B组成的系统，在细绳断开的过程中动量守恒，B与C碰撞过程中动量守恒，抓住三者最后速度相同，根据动量守恒定律求出B与C碰撞前B的速度．
（2）根据能量守恒定律求出弹簧的弹性势能．
解答：解：（1）设三者最后的共同速度为v共，由动量守恒得：
（mA+mB）v=mAv共+mBvB
mBvB=（mB+mC）v共
三者动量守恒得：（2m+m）v=（2m+m+2m）v共
得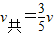
所以
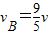
（2）弹簧释放的弹性势能
．
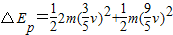
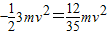答：（1）B与C碰撞前B的速度为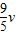
．
（2）弹簧释放的弹性势能为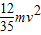
．
点评：本题综合考查了动量守恒定律和能量守恒定律，综合性较强，对学生的能力要求较高，要加强这方面的训练．
（2）根据能量守恒定律求出弹簧的弹性势能．
解答：解：（1）设三者最后的共同速度为v共，由动量守恒得：
（mA+mB）v=mAv共+mBvB
mBvB=（mB+mC）v共
三者动量守恒得：（2m+m）v=（2m+m+2m）v共
得
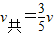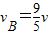
所以（2）弹簧释放的弹性势能
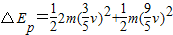
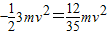．答：（1）B与C碰撞前B的速度为
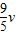．（2）弹簧释放的弹性势能为
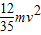．点评：本题综合考查了动量守恒定律和能量守恒定律，综合性较强，对学生的能力要求较高，要加强这方面的训练．
练习册系列答案
名校课堂系列答案
相关题目
如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上．滑轨由四部分粗细均匀的滑杆组成：水平直轨道AB；倾斜直轨道CD，长L=6m，与水平面间的夹角θ=370；半径R1=1m的圆弧轨道APC；半径R2=3m的圆弧轨道BQED．直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点．倾斜直轨道CD与小球间的动摩擦因数为μ=5/32，其余部分均为光滑轨道，取g=10m/s2，sin37°=0.6，cos37°=0.8．现让小球从AB的正中央以初速度V0=10m/s开始向左运动，问：
（2011?江苏模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中水平直轨AB与倾斜直轨CD长均为L=6m，圆弧形轨道AQC和BPD均光滑，AQC的半径为r=1m，AB、CD与两圆弧形轨道相切，O2D、O1C与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0=24J的初动能从B点开始水平向左运动，小球与两段直轨道间的动摩擦因数均为μ=
现有放置在竖直平面内游戏滑轨的模拟装置，如图所示．滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小环穿在滑轨上，以Ek0的初动能从B点开始沿BA向上运动，小环与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以初动能Ek0从B点开始沿BA向上运动，小球与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，AB、CD与两圆弧形轨道相切，BQC的半径为r=1m，APD的半径为R=2m，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=