Question

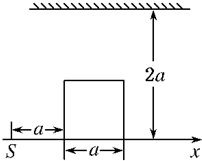如图所示，在x轴的原点放一点光源S，距点光源为a处，放一不透光的边长为a的正方体物块，若在x轴的上方距x轴为2a处放一个平行于x轴并且面向物块的长平面镜，则在x轴上正方体的右边有部分区域被镜面反射来的光照亮，当点光源沿x轴向左移动的距离至少为多少时，正方体的右侧x轴上被光照亮部分将消失（　　）

• A、

  3

  4

  a
• B、

  1

  3

  a
• C、

  1

  4

  a
• D、

  1

  2

  a

Answer 1

分析：点光源S发出的过正方体左上角射到平面镜上的光线，是光源发出的经平面镜反射后最有可能照到正方体右侧的光线，如果该光线的反射光线被正方上表面挡住，则正方体右侧照亮区将消失，作出光路图，由相似三角形的知识可求出点光源沿x轴向右移动的距离X的大小．

解答：解：当光源发出的能照到平面镜上最右侧的光恰好被正方体上表面挡住时；照亮区域将消失，根据光的反射定律作光路图如图所示．
由题意得：CD=a，SD=X+a；AE=2a-a=a，CE=

a

2

；
由图知：△CAE∽△SCD，由相似三角形的性质可得：

SD

CD

=

CE

AE

故：

a+X

a

=

a 2

a

，则X=-

a

2

；
即当点光源沿x轴向左移动的距离至少为

a

2

时，正方体的右侧x轴上被光照亮部分将消失．
故选：D．

点评：本题考查了光的反射的应用，根据题意作出光路图，应用数学知识求解本题即可．此题有一定难度，对学生的要求比较高，要求学生解答此题时，应具备较好的数学基础．