题目内容
如图,质量为M=2kg的平板小车左端放一质量为m=3kg的铁块,它与车间的动摩擦因数为m=0.5.开始车与铁块一起以v0=3m/s的速度向右在光滑水平面上运动,并与墙发生碰撞,设碰撞时间极短且无机械能损失.车身足够长.求:
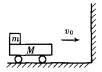
(1)铁块相对车的总位移大小.
(2)小车与墙发生第一次碰撞后所走的总路程.
答案:
解析:
解析:
(1)因m>M,故小车跟墙作多次碰撞,最后静止在墙根,系统的动能全部克服m、M间的摩擦而做功,即
所以 (2)小车第一次碰撞后向左运动,初速度仍为v0,受到摩擦力mmg的作用,速度逐渐减小至零,负加速度大小为 小车向左运动的位移为 第一次碰撞后m的速度为v0,向右.设小车与铁块的公共速度为v1,则 mv0-Mv0=(m+M)v1
故第二次碰撞后小车来回运动的路程为 依此类推,第三次碰撞后,小车来回运动的路程为 故l1,l2,l3,…,ln构成一等比数列 小车在停止前通过的总路程为
|

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
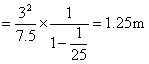
 如图所示,一质量为m的塑料球形容器放在桌面上,它的内部有一劲度系数为k的轻弹簧,弹簧直立地固定于容器内壁的底部,弹簧上端经绝缘体系住一只带正电q、质量也为m的小球.从加一个竖直向上的场强为E的匀强电场起,到容器对桌面压力减为零时为止,容器对桌面压力减为零时小球的速度大小是( )
如图所示,一质量为m的塑料球形容器放在桌面上,它的内部有一劲度系数为k的轻弹簧,弹簧直立地固定于容器内壁的底部,弹簧上端经绝缘体系住一只带正电q、质量也为m的小球.从加一个竖直向上的场强为E的匀强电场起,到容器对桌面压力减为零时为止,容器对桌面压力减为零时小球的速度大小是( ) -个质量为m的物体放在水平地面上,物体上方安装一长度为L、劲度系数为K的轻弹簧,如图所示.现用手拉着弹簧上端P点缓慢向上移动,直到物体离开地面一段距离,在这一过程中,P点的位移是h.设开始时弹簧处于自然状态,则物体重力势能的增加量为
-个质量为m的物体放在水平地面上,物体上方安装一长度为L、劲度系数为K的轻弹簧,如图所示.现用手拉着弹簧上端P点缓慢向上移动,直到物体离开地面一段距离,在这一过程中,P点的位移是h.设开始时弹簧处于自然状态,则物体重力势能的增加量为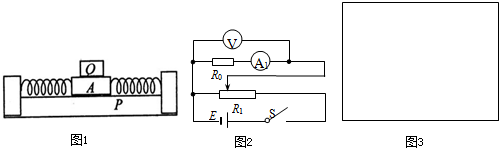
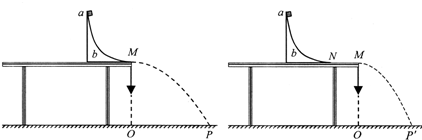
 (2013?海淀区一模)某种角速度计,其结构如图所示.当整个装置绕轴OO′转动时,元件A相对于转轴发生位移并通过滑动变阻器输出电压,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,装置静止时滑片P在变阻器的最左端B端,当系统以角速度ω转动时,则( )
(2013?海淀区一模)某种角速度计,其结构如图所示.当整个装置绕轴OO′转动时,元件A相对于转轴发生位移并通过滑动变阻器输出电压,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,装置静止时滑片P在变阻器的最左端B端,当系统以角速度ω转动时,则( )