题目内容
9. 如图所示,ABC为一透明材料做出的柱形光学元件的横截面,D为AC圆弧的圆心,∠ADC=120°,∠ABC=60°,AB=BC,B、D间的距离为d.D处点光源发出的光中有一束光线经AB、BC界面两次全反射后,光束恰好通过D点.求:
如图所示,ABC为一透明材料做出的柱形光学元件的横截面,D为AC圆弧的圆心,∠ADC=120°,∠ABC=60°,AB=BC,B、D间的距离为d.D处点光源发出的光中有一束光线经AB、BC界面两次全反射后,光束恰好通过D点.求:①该种材料折射率的最小值;
②AB上有光通过的最大长度.
分析 ①根据题意和光路的对称性,作出光路图,得到光线在AB面的入射角,由临界角公式sinC=$\frac{1}{n}$求解.
②由几何知识求出AB上有光通过的最大长度.
解答  解:①光线若能回到D点,光线如图,光线在AB面的入射角α=30°,在两个面全反射的最小折射率的临界角满足
解:①光线若能回到D点,光线如图,光线在AB面的入射角α=30°,在两个面全反射的最小折射率的临界角满足
C=α=30°
由sinC=$\frac{1}{{n}_{min}}$
解得折射率的最小值 nmin=2
②在AE段有光透过,当折射率最小时,AE段有光透过的长度最大,由几何关系知
AB=dsin60°
EB=$\frac{d}{2sin60°}$
解得AE=AB=BE=$\frac{\sqrt{3}d}{6}$
答:
①该种材料折射率的最小值是2;
②AB上有光通过的最大长度是$\frac{\sqrt{3}d}{6}$.
点评 对于几何光学中,要掌握全反射条件和临界角公式,往往要运用几何知识求解相关角度.

练习册系列答案
相关题目
19.关于物体间的作用力和反作用力,下列说法正确的是( )
| A. | 先有作用力后有反作用力 | |
| B. | 作用力和反作用力也可能作用在同一物体上 | |
| C. | 大小相等、方向相反并且在同一直线上的两个力一定是作用力和反作用力 | |
| D. | 作用力和反作用力一定大小相等、方向相反并且在同一直线上 |
20. 如图所示,理想变压器原线圈接有交流电源,副线圈上通过输电线接有灯泡Ll,L2和含有铁芯的线圈L,输电线等效电阻为R.开始时,开关S断开,滑片P处于图示位置,灯泡L1能发光.要使灯泡L1变亮,可以采取的办法是( )
如图所示,理想变压器原线圈接有交流电源,副线圈上通过输电线接有灯泡Ll,L2和含有铁芯的线圈L,输电线等效电阻为R.开始时,开关S断开,滑片P处于图示位置,灯泡L1能发光.要使灯泡L1变亮,可以采取的办法是( )
 如图所示,理想变压器原线圈接有交流电源,副线圈上通过输电线接有灯泡Ll,L2和含有铁芯的线圈L,输电线等效电阻为R.开始时,开关S断开,滑片P处于图示位置,灯泡L1能发光.要使灯泡L1变亮,可以采取的办法是( )
如图所示,理想变压器原线圈接有交流电源,副线圈上通过输电线接有灯泡Ll,L2和含有铁芯的线圈L,输电线等效电阻为R.开始时,开关S断开,滑片P处于图示位置,灯泡L1能发光.要使灯泡L1变亮,可以采取的办法是( )| A. | 向上滑动P | B. | 闭合开关S | ||
| C. | 抽出线圈中的铁芯 | D. | 增大交流电源的频率 |
17.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现,双星系统演化过程中,两星的总质量?距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,两星之间的距离变为原来的n倍,则此时圆周运动的周期为( )
| A. | $\sqrt{\frac{n}{k}}$T | B. | $\sqrt{\frac{{n}^{2}}{k}}$T | C. | $\sqrt{\frac{{n}^{3}}{{k}^{2}}}$T | D. | $\sqrt{\frac{{n}^{3}}{k}}$T |
1.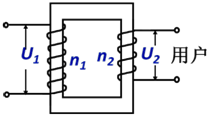 某型号变压器原副线圈匝数比为n1:n2=5:1,连接高压线变压后供电给市民,如图,则正确的是( )
某型号变压器原副线圈匝数比为n1:n2=5:1,连接高压线变压后供电给市民,如图,则正确的是( )
 某型号变压器原副线圈匝数比为n1:n2=5:1,连接高压线变压后供电给市民,如图,则正确的是( )
某型号变压器原副线圈匝数比为n1:n2=5:1,连接高压线变压后供电给市民,如图,则正确的是( )| A. | 一般家庭电路的电压为U2=220$\sqrt{2}$V | |
| B. | 如果学校实验室也接入用户交流电,则打点计时器计时周期为0.02s | |
| C. | 变压器输入的交流电频率为250Hz | |
| D. | 用多用表测量U1约为1100V |
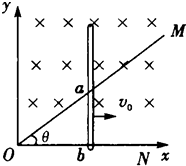 如图所示,顶角θ=45°的光滑金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r,导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触且没有脱离导轨.当t=0时,导体棒位于坐标原点o处,求:
如图所示,顶角θ=45°的光滑金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r,导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触且没有脱离导轨.当t=0时,导体棒位于坐标原点o处,求:
 如图所示,一辆质量M=3kg的小车A静止在水平面上,小车上有一质量m=1kg的小物块B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小物块与小车右壁距离为l=0.4m,解除锁定,小物块脱离弹簧后与小车右壁发生碰撞,碰撞过程无机械能损失,不计一切摩擦.求:
如图所示,一辆质量M=3kg的小车A静止在水平面上,小车上有一质量m=1kg的小物块B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小物块与小车右壁距离为l=0.4m,解除锁定,小物块脱离弹簧后与小车右壁发生碰撞,碰撞过程无机械能损失,不计一切摩擦.求: