题目内容
如图所示，在光滑固定斜面上有一个重为G的物体，若沿斜面向上和沿水平向左方向各加一个大小都为G/2的力，使物体处于平衡状态，则斜面对物体的支持力大小等于（ ）分析：选取物块为研究的对象，对物块进行受力分析，沿斜面的方向和垂直于斜面的方向分解各个力，即可求得相应的结果．
解答：
解：如图对物块进行受力分析，
沿斜面的方向：Gsinθ=
+
cosθ
整理得：2sinθ=1+cosθ ①
结合三角函数的关系：sin2θ+cos2θ=1 ②
联立①②解得：cosθ=-1 （舍去），cosθ=0.6
在垂直于斜面方向上：F=Gcosθ+
sinθ ③
联立以上各式，解得：F=G．故选项B正确．
故选：B
解：如图对物块进行受力分析，沿斜面的方向：Gsinθ=
| G |
| 2 |
| G |
| 2 |
整理得：2sinθ=1+cosθ ①
结合三角函数的关系：sin2θ+cos2θ=1 ②
联立①②解得：cosθ=-1 （舍去），cosθ=0.6
在垂直于斜面方向上：F=Gcosθ+
| G |
| 2 |
联立以上各式，解得：F=G．故选项B正确．
故选：B
点评：该题是常规的共点力平衡的题目，解题的难点在于三角函数之间的变换与求解．应属于中档题目．
练习册系列答案
相关题目
如图所示，在光滑固定的水平长杆上套着一个光滑的质量为m的滑环A，滑环通过一根不可伸长的轻绳悬吊一质量为M=3m的重物B，轻绳长为L．将滑环A固定在水平杆上，给B一个水平瞬时冲量作用，使B向左摆动，且恰好刚碰到水平杆．若滑环A不固定，仍给B以同样大小的冲量作用，在此后的运动过程中，求：
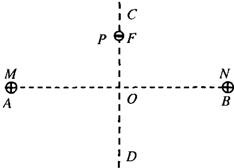如图所示，在光滑绝缘水平面上，两个带等量正电的点电荷M、N，分别固定在A、B两点，O为AB连线的中点，CD为AB的垂直平分线．在CO之间的F点由静止释放一个带负电的小球P（设不改变原来的电场分布），在以后的一段时间内，P在CD连线上做往复运动．若（ ）| A、小球P的带电量缓慢减小，则它往复运动过程中振幅不断减小 | B、小球P的带电量缓慢减小，则它往复运动过程中每次经过O点时的速率不断减小 | C、点电荷M、N的带电量同时等量地缓慢增大，则小球P往复运动过程中周期不断减小 | D、点电荷M、N的带电量同时等量地缓慢增大，则小球P往复运动过程中振幅不断减小 |
（2013?郑州二模）如图所示，在光滑的水平地面上有一个表面光滑的立方体Q一长为L的轻杆下端用光滑铰链连接于O点，O点固定于地面上，轻杆的上端连接着一个可视为质点的小球P，小球靠在立方体左侧，P和Q的质量相等，整个装置处于静止状态．受到轻微扰动后P倒向右侧并推动Q．下列说法中正确的是（ ）