题目内容
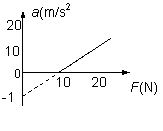
 在某地竖直向上提升重物,不计阻力,加速度a与拉力F之间的关系如图所示,该地重力加速度大小约为
在某地竖直向上提升重物,不计阻力,加速度a与拉力F之间的关系如图所示,该地重力加速度大小约为分析:物体受重力和拉力,根据牛顿第二定律列式求解加速度与拉力关系的表达式,结合图象得到物体的质量和重力加速度;物体匀加速上升后,先根据运动学公式求解加速度,再根据牛顿第二定律求解拉力.
解答:解:在某地竖直向上提升重物,不计阻力,物体受重力和拉力,根据牛顿第二定律,有:
F-mg=ma
解得:a=
-g
结合图象,纵轴截距表示-g,故g=10m/s2
结合图象,斜率表示质量的倒数,故:
=1,m=1kg;
该重物从地面被竖直提起后作匀加速运动,2s末达到8m高度,根据位移时间关系公式,有:
h=
at2;
解得:a=
=
=4m/s2;
根据牛顿第二定律,有:
F-mg=ma
解得:F=m(g+a)=1×(10+4)=14N;
故答案为:10,14.
F-mg=ma
解得:a=
| F |
| m |
结合图象,纵轴截距表示-g,故g=10m/s2
结合图象,斜率表示质量的倒数,故:
| 1 |
| m |
该重物从地面被竖直提起后作匀加速运动,2s末达到8m高度,根据位移时间关系公式,有:
h=
| 1 |
| 2 |
解得:a=
| 2h |
| t2 |
| 2×8 |
| 22 |
根据牛顿第二定律,有:
F-mg=ma
解得:F=m(g+a)=1×(10+4)=14N;
故答案为:10,14.
点评:重点是对图象的识别,由于不同图象其坐标轴含义不一样,图象问题一般重点掌握以下几点的含义:起点,交点,终点,斜率.准确掌握以上几点,才能正确应对图象问题.

练习册系列答案
相关题目