题目内容
10. 如图所示,一质量为m的小物块从P点静止释放,下降2R的距离后,沿着半径为R的四分之一圆弧轨道上与圆心等高的A点的切线方向进入圆弧轨道,经过轨道最低点B时对轨道压力大小为5mg,不计空气阻力.求:
如图所示,一质量为m的小物块从P点静止释放,下降2R的距离后,沿着半径为R的四分之一圆弧轨道上与圆心等高的A点的切线方向进入圆弧轨道,经过轨道最低点B时对轨道压力大小为5mg,不计空气阻力.求:(1)小物块到达B点瞬间的速度大小v;
(2)小物块在圆弧轨道上运动过程中克服摩擦阻力做功Wf.
分析 (1)根据在圆周轨道最低点小球在竖直方向的合力提供圆周运动向心力求得小球的速度大小;
(2)小球在运动过程中只有重力和圆弧轨道的摩擦力做功,根据动能定理求得摩擦力做的功即可.
解答 解:(1)小物块在B点在圆周运动,
由牛顿第二定律得:$N-mg=m\frac{{v}^{2}}{R}$,
由题意可知:N=5mg,
解得:$v=\sqrt{\frac{(N-mg)R}{m}}=\sqrt{\frac{(5mg-mg)R}{m}}=2\sqrt{gR}$;
(2)P到B过程中有重力做功和AB段轨道摩擦力对小球做功,由动能定理得:
$mg•3R+{W}_{f}=\frac{1}{2}m{v}^{2}-0$
解得:${W}_{f}=\frac{1}{2}m{v}^{2}-3mgR$=-mgR
所以在圆弧轨道上小物块克服摩擦力做的功为mgR.
答:(1)小物块到达B点瞬间的速度大小v为$2\sqrt{gR}$;
(2)小物块在圆弧轨道上运动过程中克服摩擦阻力做功Wf为mgR.
点评 本题考查了求速度、功问题,分析清楚物块的运动过程、应用牛顿第二定律、动能定理求解是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.在物理学发展过程中,许多物理学家做出了杰出贡献,下列说法中错误的是( )
| A. | 奥斯特发现了电流的磁效应 | |
| B. | 安培首先总结了电路中电流与电压和电阻的关系 | |
| C. | 洛仑兹发现了磁场对运动电荷的作用规律 | |
| D. | 法拉第对电磁感应现象进行了丰富的、开创性的研究 |
5. 如图所示,球A重G1,斜面体B重G2,斜面倾角为θ,一切摩擦均不计.使A、B均处于静止状态,下列说法正确的是( )
如图所示,球A重G1,斜面体B重G2,斜面倾角为θ,一切摩擦均不计.使A、B均处于静止状态,下列说法正确的是( )
 如图所示,球A重G1,斜面体B重G2,斜面倾角为θ,一切摩擦均不计.使A、B均处于静止状态,下列说法正确的是( )
如图所示,球A重G1,斜面体B重G2,斜面倾角为θ,一切摩擦均不计.使A、B均处于静止状态,下列说法正确的是( )| A. | 水平力F为$\frac{{G}_{1}}{cosθ}$ | B. | 竖直墙壁对A的弹力等于F | ||
| C. | 水平地面受到的弹力为G1+G2 | D. | A对B的弹力等于G1tanθ |
15.关于牛顿第一定律,下列说法正确的是( )
| A. | 牛顿第一定律是一条实验定律 | |
| B. | 牛顿第一定律说明了力是改变物体运动状态的原因 | |
| C. | 惯性定律和惯性的实质是相同的 | |
| D. | 物体的运动需要力来维持 |
2. 如图所示,同步卫星与地心的距离为r,运行速率为v1,向心加速度为a1;地球赤道上的物体随地球白转的向心加速度为a2,第一宇宙速度为v2.已知地球质量为M,地球半径为R,引力常量为G.则下列关系式正确的是( )
如图所示,同步卫星与地心的距离为r,运行速率为v1,向心加速度为a1;地球赤道上的物体随地球白转的向心加速度为a2,第一宇宙速度为v2.已知地球质量为M,地球半径为R,引力常量为G.则下列关系式正确的是( )
 如图所示,同步卫星与地心的距离为r,运行速率为v1,向心加速度为a1;地球赤道上的物体随地球白转的向心加速度为a2,第一宇宙速度为v2.已知地球质量为M,地球半径为R,引力常量为G.则下列关系式正确的是( )
如图所示,同步卫星与地心的距离为r,运行速率为v1,向心加速度为a1;地球赤道上的物体随地球白转的向心加速度为a2,第一宇宙速度为v2.已知地球质量为M,地球半径为R,引力常量为G.则下列关系式正确的是( )| A. | R${\;}_{{v}_{1}}$=rv2 | B. | M=$\frac{{a}_{1}{r}^{2}}{G}$ | C. | a1r2=a2R2 | D. | v2=$\sqrt{{a}_{2}R}$ |
19.某中学正在举行班级对抗赛,张明明同学是短跑运动员,在百米竞赛中,测得他在5s末的速度为10.5m/s,10s末到达终点的速度为10.8m/s,则他在全程中的平均速度为( )
| A. | 10.4 m/s | B. | 10.3 m/s | C. | 10.2 m/s | D. | 10m/s |
20.在赤道上空,一根沿东西方向的水平导线自由下落,则导线上各点的电势正确的说法是( )
| A. | 东端低 | B. | 西端低 | C. | 各点电势相同 | D. | 无法判断 |
 一个半径为r、质量为m的重球用长度等于r的绳子挂在竖直的光滑墙壁A处(如图),求:
一个半径为r、质量为m的重球用长度等于r的绳子挂在竖直的光滑墙壁A处(如图),求: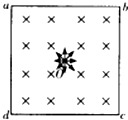 如图所示,在正方形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场.在t=0时刻,一位于正方形区域中心O的粒子源在abcd平面内向各个方向发射出大量带正电的同种粒子,所有粒子的初速度大小均相同,粒子在磁场中做圆周运动的半径恰好等于正方形边长,不计重力和粒子之间的相互作用力.已知平行于ad方向发射的粒子在t=t0时刻刚好从磁场边界cd上的某点离开磁场,(已知sin$\frac{23π}{200}$=$\frac{\sqrt{2}}{4}$)求:
如图所示,在正方形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场.在t=0时刻,一位于正方形区域中心O的粒子源在abcd平面内向各个方向发射出大量带正电的同种粒子,所有粒子的初速度大小均相同,粒子在磁场中做圆周运动的半径恰好等于正方形边长,不计重力和粒子之间的相互作用力.已知平行于ad方向发射的粒子在t=t0时刻刚好从磁场边界cd上的某点离开磁场,(已知sin$\frac{23π}{200}$=$\frac{\sqrt{2}}{4}$)求: