题目内容
如图所示,质量满足mA=2mB=3mC的三个物块A、B、C,A与天花板之间、B与C之间均用轻弹簧相连,A与B之间用细绳相连,当系统静止后,突然剪断AB间的细绳,则此瞬间A、B、C的加速度分别为(取向下为正)( )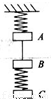
A.-
 g、2g、0
g、2g、0B.-2g、2g、0
C.-
 g、
g、 g、0
g、0D.-2g、
 g、g
g、g
【答案】分析:本题考查了瞬间加速度的计算,弹簧弹力不能发生突变,在剪短瞬间仍然保持原来的大小和方向;而细绳的弹力会发生突变,在剪断瞬间会突然改变;剪断细线前对A、B和C整体物体分别受力分析,根据平衡条件求出细线的弹力,断开细线后,再分别对A、B和C整体受力分析,求解出合力并运用牛顿第二定律求解加速度.
解答:解:设C物体的质量为m,则A物体的质量为3m,B物体的质量为1.5m,
剪断细线前,对BC整体受力分析,受到总重力和细线的拉力而平衡,故T=2.5mg;
再对物体A受力分析,受到重力、细线拉力和弹簧的拉力;
剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体A受到的力的合力等于2.5mg,向上,
根据牛顿第二定律得A的加速度为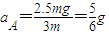 ①
①
物体C受到的力不变,合力为零,故C的加速度为aC=0 ②
剪断细线前B受重力、绳子的拉力和弹簧的拉力,他们合力为零;
剪短细线后,绳子的拉力突变为零,重力和弹簧的弹力不变,故B合力大小等于绳子的拉力2.5mg,方向竖直向下,
根据牛顿第二定律得B的加速度为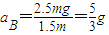 ③
③
根据①②③式知ABD错误,C正确;
故选C.
点评:本题是力学中的瞬时问题,关键是先根据平衡条件求出各个力,然后根据牛顿第二定律列式求解加速度;同时要注意轻弹簧的弹力与形变量成正比,来不及突变,而细线的弹力是有微小形变产生的,故可以突变.
解答:解:设C物体的质量为m,则A物体的质量为3m,B物体的质量为1.5m,
剪断细线前,对BC整体受力分析,受到总重力和细线的拉力而平衡,故T=2.5mg;
再对物体A受力分析,受到重力、细线拉力和弹簧的拉力;
剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体A受到的力的合力等于2.5mg,向上,
根据牛顿第二定律得A的加速度为
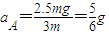 ①
①物体C受到的力不变,合力为零,故C的加速度为aC=0 ②
剪断细线前B受重力、绳子的拉力和弹簧的拉力,他们合力为零;
剪短细线后,绳子的拉力突变为零,重力和弹簧的弹力不变,故B合力大小等于绳子的拉力2.5mg,方向竖直向下,
根据牛顿第二定律得B的加速度为
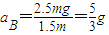 ③
③根据①②③式知ABD错误,C正确;
故选C.
点评:本题是力学中的瞬时问题,关键是先根据平衡条件求出各个力,然后根据牛顿第二定律列式求解加速度;同时要注意轻弹簧的弹力与形变量成正比,来不及突变,而细线的弹力是有微小形变产生的,故可以突变.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 如图所示,质量为M=1Kg的长滑块B静止放在光滑的水平地面上,左边固定一劲度系数为K=8N/m且足够长的水平轻质弹簧,右侧有一不可伸长的轻绳连接于竖直墙壁上,细线所能承受的最大拉力为T=4N.现使一质量为m=2Kg,初速度为v0的小物体A,在滑块B上无摩擦地向左运动,而后压缩弹簧.(已知弹簧的弹性势能EP与弹簧的形变量x的关系:
如图所示,质量为M=1Kg的长滑块B静止放在光滑的水平地面上,左边固定一劲度系数为K=8N/m且足够长的水平轻质弹簧,右侧有一不可伸长的轻绳连接于竖直墙壁上,细线所能承受的最大拉力为T=4N.现使一质量为m=2Kg,初速度为v0的小物体A,在滑块B上无摩擦地向左运动,而后压缩弹簧.(已知弹簧的弹性势能EP与弹簧的形变量x的关系:
 (2010?如皋市模拟)如图所示,质量为M的长滑块静止在光滑水平地面上,左端固定一劲度系数为k足够长的水平轻质弹簧,右侧用一不可伸长的细绳连接于竖直墙上,细绳所能承受的最大拉力为FT,使一质量为m、初速度为Vo的小物体,在滑块上无摩擦地向左滑动而后压缩弹簧,已知弹簧的弹性势能表达式为Ep=kx2*1/2(k为弹簧的劲度系数,x为弹簧的形变量).
(2010?如皋市模拟)如图所示,质量为M的长滑块静止在光滑水平地面上,左端固定一劲度系数为k足够长的水平轻质弹簧,右侧用一不可伸长的细绳连接于竖直墙上,细绳所能承受的最大拉力为FT,使一质量为m、初速度为Vo的小物体,在滑块上无摩擦地向左滑动而后压缩弹簧,已知弹簧的弹性势能表达式为Ep=kx2*1/2(k为弹簧的劲度系数,x为弹簧的形变量). (2012?湖南模拟)如图所示,质量为M的三角形木块A静止在水平面上.一质量为m的物体B正沿A的斜面下滑,三角形木块A仍然保持静止.则下列说法中正确的是( )
(2012?湖南模拟)如图所示,质量为M的三角形木块A静止在水平面上.一质量为m的物体B正沿A的斜面下滑,三角形木块A仍然保持静止.则下列说法中正确的是( ) 如图所示,质量为m=60Kg,重心离地面高度为H=0.8m的运动员进行“挑战极限运动”训练,需穿越宽为s1=2.5m的水沟并落到高为h=2.0m的平台上.运动员手握长为L=3.25m轻质弹性杆一端,从A点静止开始匀加速助跑,至B点时(从A到B过程中可以认为人一直是直立的)将杆的一端抵在O点的障碍物上,杆发生形变,同时运动员蹬地后被弹起,到达最高点时杆处于竖直状态,且重心恰好在杆的顶端,此刻运动员放开杆水平飞出并趴(人的重心直接落在保护垫上)在平台的保护垫上,忽略空气阻力,取g=10m/s2.
如图所示,质量为m=60Kg,重心离地面高度为H=0.8m的运动员进行“挑战极限运动”训练,需穿越宽为s1=2.5m的水沟并落到高为h=2.0m的平台上.运动员手握长为L=3.25m轻质弹性杆一端,从A点静止开始匀加速助跑,至B点时(从A到B过程中可以认为人一直是直立的)将杆的一端抵在O点的障碍物上,杆发生形变,同时运动员蹬地后被弹起,到达最高点时杆处于竖直状态,且重心恰好在杆的顶端,此刻运动员放开杆水平飞出并趴(人的重心直接落在保护垫上)在平台的保护垫上,忽略空气阻力,取g=10m/s2.