题目内容
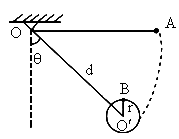
如图所示,长为L不可伸长的经绳,一端固定于O点,另一端系一质量为m的小球.最初小球位于A点,细绳伸直且水平,由静止将小球释放,小球将在竖直面内摆动,若预先在该平面内钉一个小钉子于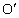 点,
点,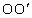 与竖直方向夹角为θ,为使小球能绕
与竖直方向夹角为θ,为使小球能绕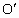 点在竖直面内做圆周运动,
点在竖直面内做圆周运动, 的距离应满足什么条件?
的距离应满足什么条件?
答案:略
解析:
解析:
|
d=3L/(3+2cosθ) 在小球运动过程中,小球受重力和轻绳拉力作用,拉力方向始终与运动方向垂直,故在小球的运动过程中只有重力对它做功,满足机械能守恒定律.另外,要使小球能绕 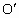 点在竖直面内做圆周运动,也就是小球在小圆最高点B点不掉下来,此时轻绳结小球拉力恰为零,由重力提供小球在B点的向心力. 点在竖直面内做圆周运动,也就是小球在小圆最高点B点不掉下来,此时轻绳结小球拉力恰为零,由重力提供小球在B点的向心力.
选取 A点所在的水平面为参考面,则有:
由机械能守恒定律得:
由牛顿第二定律得: 由几何关系得:d+r=L③ 由①②③三式解得:d=3L/(3+2cosθ). 在应用机械能守恒定律的一船表达式解题时,注意重力势能零参考面的选取,选得巧,可使求解过种变得容易. |

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 ,
,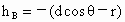
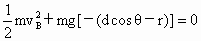 ①
①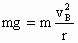 ②
② (2011?茂名一模)如图所示,长为L的不可伸长的绳子一端固定在O点,另一端系质量为m的小球,小球静止在光滑水平面上.现用大小为F水平恒力作用在另一质量为2m的物块上,使其从静止开始向右运动,一段时间后撤去该力,物块与小球发生正碰后速度变为原来的一半,小球恰好能在竖直平面内做圆周运动.已知重力加速度为g,小球和物体均可视为质点,试求:
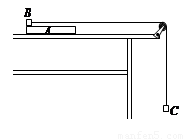
(2011?茂名一模)如图所示,长为L的不可伸长的绳子一端固定在O点,另一端系质量为m的小球,小球静止在光滑水平面上.现用大小为F水平恒力作用在另一质量为2m的物块上,使其从静止开始向右运动,一段时间后撤去该力,物块与小球发生正碰后速度变为原来的一半,小球恰好能在竖直平面内做圆周运动.已知重力加速度为g,小球和物体均可视为质点,试求: (2011?双流县模拟)如图所示,长为L的木板A静止在光滑的水平桌面上,A的左端上方放有小物体B(可视为质点),一端连在B上的细绳,绕过固定在桌子边沿的定滑轮后,另一端连在小物体C上,设法用外力使A、B静止,此时C被悬挂着.A的右端距离滑轮足够远,C距离地面足够高.已知A的质量为6m,B的质量为3m,C的质量为m.现将C物体竖直向上提高距离2L,同时撤去固定A、B的外力.再将C无初速释放,当细绳被拉直时B、C速度的大小立即变成相等,由于细绳被拉直的时间极短,此过程中重力和摩擦力的作用可以忽略不计,细绳不可伸长,且能承受足够大的拉力.最后发现B在A上相对A滑行的最大距离为
(2011?双流县模拟)如图所示,长为L的木板A静止在光滑的水平桌面上,A的左端上方放有小物体B(可视为质点),一端连在B上的细绳,绕过固定在桌子边沿的定滑轮后,另一端连在小物体C上,设法用外力使A、B静止,此时C被悬挂着.A的右端距离滑轮足够远,C距离地面足够高.已知A的质量为6m,B的质量为3m,C的质量为m.现将C物体竖直向上提高距离2L,同时撤去固定A、B的外力.再将C无初速释放,当细绳被拉直时B、C速度的大小立即变成相等,由于细绳被拉直的时间极短,此过程中重力和摩擦力的作用可以忽略不计,细绳不可伸长,且能承受足够大的拉力.最后发现B在A上相对A滑行的最大距离为 如图所示,长为L的轻杆一端固定着质量为m的小球绕另一端O在竖直平面内做圆周运动,则下列说法中正确的是( )
如图所示,长为L的轻杆一端固定着质量为m的小球绕另一端O在竖直平面内做圆周运动,则下列说法中正确的是( )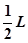 。细绳始终在滑轮上,不计滑轮与细绳之间的摩擦,计算中可认为A、B之间的最大静摩擦力等于滑动摩擦力。(取g=10m/s2)
。细绳始终在滑轮上,不计滑轮与细绳之间的摩擦,计算中可认为A、B之间的最大静摩擦力等于滑动摩擦力。(取g=10m/s2)