题目内容
18. 如图所示,由斜面AB和圆弧BCD组成的轨道在竖直平面内,AB和BCD刚好在B点相切,斜面AB长L=1m,倾角θ=53°,圆轨道半径R=0.2m,直径CD与水平面垂直,一质量m=0.1kg的小球(可视为质点)从斜面顶端A点由静止释放,取g=10m/s2,sin53°=0.8,cos53°=0.6.
如图所示,由斜面AB和圆弧BCD组成的轨道在竖直平面内,AB和BCD刚好在B点相切,斜面AB长L=1m,倾角θ=53°,圆轨道半径R=0.2m,直径CD与水平面垂直,一质量m=0.1kg的小球(可视为质点)从斜面顶端A点由静止释放,取g=10m/s2,sin53°=0.8,cos53°=0.6.(1)若轨道光滑,求小球滑到斜面底端B时的速度大小vB以及到最低点C时对圆轨道的压力大小FC;
(2)若轨道粗糙,且小球到达圆弧最高点D时对轨道压力恰好为零,求小球从A点运动到D点的过程中克服阻力做的功Wf.
分析 (1)若轨道光滑,小球沿倾斜轨道下滑时,只有重力对物块做功,根据动能定理求得小物块滑到B点和C点时的速度;由牛顿第二定律求得在C点时轨道对小球的支持力,从而得到小球对轨道的压力大小;
(2)小球到达圆弧最高点D时对轨道压力恰好为零,由重力充当向心力,由牛顿第二定律求得C点的速度,再根据动能定理求解.
解答 解:(1)小球沿斜面下滑时只有重力做功,根据动能定理可得:
A到B过程有:mgLsinθ=$\frac{1}{2}m{v}_{B}^{2}$-0
由此代入数据可解得:vB=$\sqrt{2gLsinθ}$=4m/s;
A到C过程有:mgLsinθ+mgR(1-cosθ)=$\frac{1}{2}m{v}_{C}^{2}$
在C点,由牛顿第二定律得
FC′-mg=m$\frac{{v}_{C}^{2}}{R}$
可得 FC′=9.8N
由牛顿第三定律得,到最低点C时对圆轨道的压力大小FC=FC′=9.8N
(3)小球到达圆弧最高点D时对轨道压力恰好为零,由重力充当向心力,由牛顿第二定律得
mg=m$\frac{{v}_{D}^{2}}{R}$
从A到D,由动能定理得
mg[Lsinθ-R(1+cosθ)]-Wf=$\frac{1}{2}m{v}_{D}^{2}$-0
解得 Wf=0.38J
答:
(1)小球滑到斜面底端B时的速度大小vB是4m/s,最低点C时对圆轨道的压力大小FC是9.8N.
(2)小球从A点运动到D点的过程中克服阻力做的功Wf为0.38J.
点评 正确的对物体进行受力分析和做功分析,由动能定理求解物体的速度,掌握竖直面内圆周运动通过最高点的临界条件是正确解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列不属于曲线运动的是( )
| A. | 汽车在平直的公路上行驶 | B. | 地球绕着太阳转 | ||
| C. | 小明绕着操场跑步 | D. | 电子绕着原子核运转 |
9.关于运动的合成与分解,下列说法中正确的是( )
| A. | 两个速度大小不等的匀速直线运动的合运动一定是匀速直线运动 | |
| B. | 两个直线运动的合运动一定是直线运动 | |
| C. | 合速度大小可以小于分速度大小 | |
| D. | 由两个分速度的大小就可以确定合运动速度的大小 |
3.当分子间距离大于10r0(r0是分子平衡位置间距离)时,分子力可以认为是零,规定此时分子势能为零,当分子间距离是平衡距离r0时,下面的说法中正确的是( )
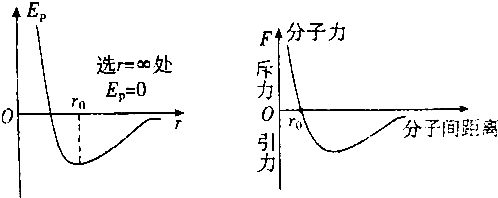

| A. | 分子力是零,分子势能也是零 | B. | 分子力是零,分子势能不是零 | ||
| C. | 分子力不是零,分子势能是零 | D. | 分子力不是零,分子势能不是零 |
8.某同学蹲在体重计上,用力向上提体重计,则此时( )
| A. | 体重计示数将变小 | |
| B. | 体重计示数将变大 | |
| C. | 体重计示数不变 | |
| D. | 如果力足够大,体重计和人会被一起提起 |
 如图,用干涉法检查工件表面的平整度时,产生的干涉条纹是一组平行的直线,若劈尖的上表面向上平移,干涉条纹将不变(填“变窄”、“变宽”或“不变”,下同);若使劈尖的角度增大,干涉条纹将变窄;.若用折射率为n的透明介质充满劈尖.干涉条纹将变窄.
如图,用干涉法检查工件表面的平整度时,产生的干涉条纹是一组平行的直线,若劈尖的上表面向上平移,干涉条纹将不变(填“变窄”、“变宽”或“不变”,下同);若使劈尖的角度增大,干涉条纹将变窄;.若用折射率为n的透明介质充满劈尖.干涉条纹将变窄. 竖直平面内的轨道ABCD由水平滑道AB与光滑的四分之一圆弧滑道CD组成,AB恰与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平滑道AB,沿着轨道运动,由DC弧滑下后停在水平滑道AB的中点.已知水平滑道AB长为L,轨道ABCD的质量为3m.求:
竖直平面内的轨道ABCD由水平滑道AB与光滑的四分之一圆弧滑道CD组成,AB恰与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平滑道AB,沿着轨道运动,由DC弧滑下后停在水平滑道AB的中点.已知水平滑道AB长为L,轨道ABCD的质量为3m.求: 两个宪全相同的物块A、B,在同一粗糙水平面上以不同的初速度从同一位置开始运动.图中两条直线分别表示物块受到水平拉力作用和不受拉力作用的v-t图象.求:
两个宪全相同的物块A、B,在同一粗糙水平面上以不同的初速度从同一位置开始运动.图中两条直线分别表示物块受到水平拉力作用和不受拉力作用的v-t图象.求: