题目内容
8.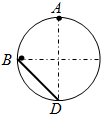 如图所示,将小球甲、乙(都可视为质点)分别从A、B两点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D.如果忽略一切摩擦阻力,那么下列判断正确的是( )
如图所示,将小球甲、乙(都可视为质点)分别从A、B两点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D.如果忽略一切摩擦阻力,那么下列判断正确的是( )| A. | 甲、乙同时到达D点 | B. | 甲球最先到达D点 | ||
| C. | 乙球最先到达D点 | D. | 无法判断哪个球先到达D点 |
分析 A为自由落体,运用自由落体的公式求出时间,B是利用匀变速运动的知识求出所用时间,
解答 解:A点,AD距离为2r,加速度为g,时间为:${t}_{1}=\sqrt{\frac{4r}{g}}$=$2\sqrt{\frac{r}{g}}$;
B点,设∠ADB=θ,BD距离为2rcosθ,加速度为gcosθ,时间为:${t}_{2}=\sqrt{\frac{4rcosθ}{gcosθ}}=\sqrt{\frac{4r}{g}}$=$2\sqrt{\frac{r}{g}}$;
故选:A
点评 解得本题的关键是分清两种不同的运动形态,然后分别计算出每条线路所用的时间,比较大小皆可解决

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18. 矩形导线框abcd固定在匀强磁场中(如图甲),磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间t变化的规律如图乙,则( )
矩形导线框abcd固定在匀强磁场中(如图甲),磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间t变化的规律如图乙,则( )
 矩形导线框abcd固定在匀强磁场中(如图甲),磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间t变化的规律如图乙,则( )
矩形导线框abcd固定在匀强磁场中(如图甲),磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间t变化的规律如图乙,则( )| A. | 从0到t1时间内,导线框中电流越来越小 | |
| B. | 从0到t1时间内,导线框中电流的方向为adcba | |
| C. | 从t1到t2时间内,导线框中电流越来越大 | |
| D. | 从t1到t2时间内,导线框bc边受到安培力大小保持不变 |
3. 如图甲所示是回旋加速器的示意图,其核心部分是两个置于匀强磁场中的D形金属盒,两盒分别与高频电源相连.带电粒子在加速时,其动能Ek随时间t的变化规律如图乙所示,忽略带电粒子在电场中的加速时间,则下列判断正确的是( )
如图甲所示是回旋加速器的示意图,其核心部分是两个置于匀强磁场中的D形金属盒,两盒分别与高频电源相连.带电粒子在加速时,其动能Ek随时间t的变化规律如图乙所示,忽略带电粒子在电场中的加速时间,则下列判断正确的是( )
 如图甲所示是回旋加速器的示意图,其核心部分是两个置于匀强磁场中的D形金属盒,两盒分别与高频电源相连.带电粒子在加速时,其动能Ek随时间t的变化规律如图乙所示,忽略带电粒子在电场中的加速时间,则下列判断正确的是( )
如图甲所示是回旋加速器的示意图,其核心部分是两个置于匀强磁场中的D形金属盒,两盒分别与高频电源相连.带电粒子在加速时,其动能Ek随时间t的变化规律如图乙所示,忽略带电粒子在电场中的加速时间,则下列判断正确的是( )| A. | 在Ek-t图象中应有(t4-t3)<(t3-t2)<(t2-t1) | |
| B. | 高频电源的变化周期应该等于tn-tn-1 | |
| C. | 要想粒子获得的最大动能增大,可增加D形盒的半径 | |
| D. | 加速电场的电压越大,则粒子获得的最大动能一定越大 |
13.下列关于与电场强度有关的几个公式的说法中,正确的是( )
| A. | 公式U=Ed只适用于匀强电场 | |
| B. | 只要电场中电场线是直线,公式U=Ed就适用 | |
| C. | 公式E=$\frac{F}{q}$是电场强度的定义式,适用于任何电场 | |
| D. | 公式E=$\frac{Kq}{{r}^{2}}$是由库仑定律得出的,因而只适用于点电荷(真空中)的电场 |
18.如图所示,小物块位于半径为R的半球形物体顶端,若给小物块一水平速度v0=$\sqrt{2gR}$,则物块( )


| A. | 沿球体表面做圆周运动 | B. | 落地时水平位移为$\sqrt{2}R$ | ||
| C. | 落地速度大小为$\sqrt{gR}$ | D. | 落地时速度方向与地面成45°角 |
 某兴趣小组对一火灾报警装置的部分电路进行探究,其电路图如图甲所示,其中R2是半导体热敏电阻,它的电阻随温度变化关系如图乙所示.当R2所在处出现火情时,通过电流表的电流I和a、b间端电压U与出现火情前相比,电流表的电流I增大 (填增大、减小、不变);a、b间端电压U减小 (填增大、减小、不变).
某兴趣小组对一火灾报警装置的部分电路进行探究,其电路图如图甲所示,其中R2是半导体热敏电阻,它的电阻随温度变化关系如图乙所示.当R2所在处出现火情时,通过电流表的电流I和a、b间端电压U与出现火情前相比,电流表的电流I增大 (填增大、减小、不变);a、b间端电压U减小 (填增大、减小、不变). 长L=1m、质量可忽略的杆,其下端固定于O点,上端连有质量m=2kg的小球,它绕O点做圆周运动,当通过最高点时,如图所示,求下列情况下杆受到的力的大小和方向.
长L=1m、质量可忽略的杆,其下端固定于O点,上端连有质量m=2kg的小球,它绕O点做圆周运动,当通过最高点时,如图所示,求下列情况下杆受到的力的大小和方向.



