题目内容
11.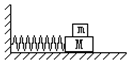 在如图所示的系统中,弹簧劲度系数k=39.2N/m,与弹簧相连的物块M质量为0.2kg,置于其上的物块m质量为0.1kg.两物体之间的最大静摩擦力fm=0.196N,M与水平支持面之间是光滑的.若要使两物块一起(两物块之间无相对滑动)做简谐运动,则
在如图所示的系统中,弹簧劲度系数k=39.2N/m,与弹簧相连的物块M质量为0.2kg,置于其上的物块m质量为0.1kg.两物体之间的最大静摩擦力fm=0.196N,M与水平支持面之间是光滑的.若要使两物块一起(两物块之间无相对滑动)做简谐运动,则(1)请画出在左端最大振幅处两个物体的受力分析;
(2)可能达到的最大振幅是多大;
(3)从2问中最大振幅处向平衡位置运动过程中,摩擦力对m做的功.
分析 (1)分别对m与M进行受力分析,然后画出受力图即可;
(2)在最大位移处,加速度最大,静摩擦力最大,根据牛顿第二定律列方程即可;
(3)在物块向平衡位置运动的过程中,弹簧的弹性势能转化为物块的动能,由此计算出M与m的速度;m逐渐的动能等于摩擦力对M做的功,由动能定理即可求出.
解答  解:(1)在左端时,m受到重力、支持力以及摩擦力的作用,如图1;
解:(1)在左端时,m受到重力、支持力以及摩擦力的作用,如图1;
在最左端时,M受到重力、地面的支持力、m的压力、弹簧的推力以及m对M的摩擦力,如图2;
(2)由此考虑临界状态,即m正好不发生打滑,这种情况下的振幅就是所求的最大振幅.
此时m 受最大静摩擦力的作用,对m:fm=ma
对整体分析,M和m这一系统受到的合力就是弹簧的作用力,即F=kA,
由牛顿运动定律得:
对整体:kA=(M+m)a
得到系统振动的最大振幅为:$A=\frac{(M+m){f}_{m}}{km}$
代入数据得:A=0.15m
(3)在物块向平衡位置运动的过程中,弹簧的弹性势能转化为物块的动能,得:
$\frac{1}{2}(M+m){v}^{2}=\frac{1}{2}k{A}^{2}$
m受到的摩擦力对m做的功转化为m的动能,由动能定理得:
${W}_{f}=\frac{1}{2}m{v}^{2}$
代入数据联立得:Wf=0.147J
答:(1)如图;
(2)该系统振动的最大振幅是0.015m;
(3)摩擦力对m做的功是0.147J.
点评 本题关键明确当位移x变大时,静摩擦力变大,然后根据牛顿第二定律并结合整体法和隔离法列式求解.

练习册系列答案
相关题目
19.关于交流电路中的扼流圈,下列说法正确的是( )
| A. | 扼流圈是利用电感线圈对交流的阻碍作用来工作的 | |
| B. | 高频扼流圈的作用是允许低频交流通过,而阻碍高频交流通过 | |
| C. | 低频扼流圈的作用是不仅要阻碍高频交流通过,还要阻碍低频交流通过 | |
| D. | 高频扼流圈的电感比低频扼流圈的电感大 |
20. 2017年4月22日,我国首艘货运飞船“天舟一号”与“天宫二号”空间实验室完成交会对接.若飞船绕地心做匀速圆周运动,距离地面的高度为h,地球半径为R,地球表面的重力加速度为g,引力常量为G.下列说法正确的是( )
2017年4月22日,我国首艘货运飞船“天舟一号”与“天宫二号”空间实验室完成交会对接.若飞船绕地心做匀速圆周运动,距离地面的高度为h,地球半径为R,地球表面的重力加速度为g,引力常量为G.下列说法正确的是( )
 2017年4月22日,我国首艘货运飞船“天舟一号”与“天宫二号”空间实验室完成交会对接.若飞船绕地心做匀速圆周运动,距离地面的高度为h,地球半径为R,地球表面的重力加速度为g,引力常量为G.下列说法正确的是( )
2017年4月22日,我国首艘货运飞船“天舟一号”与“天宫二号”空间实验室完成交会对接.若飞船绕地心做匀速圆周运动,距离地面的高度为h,地球半径为R,地球表面的重力加速度为g,引力常量为G.下列说法正确的是( )| A. | 根据题中条件可以估算飞船的质量 | |
| B. | 天舟一号飞船内的货物处于平衡状态 | |
| C. | 飞船在圆轨道上运行的加速度为$\frac{{g{R^2}}}{{{{(R+h)}^2}}}$ | |
| D. | 飞船在圆轨道上运行的速度大小为 $R\sqrt{\frac{g}{R+h}}$ |
9. 如图所示,匀强电场中的A、B、C、D点构成一位于纸面内平行四边形,电场强度的方向与纸面平行,已知A、B两点的电势分别为φA=12V、φB=6V,则C、D两点的电势可能分别为( )
如图所示,匀强电场中的A、B、C、D点构成一位于纸面内平行四边形,电场强度的方向与纸面平行,已知A、B两点的电势分别为φA=12V、φB=6V,则C、D两点的电势可能分别为( )
 如图所示,匀强电场中的A、B、C、D点构成一位于纸面内平行四边形,电场强度的方向与纸面平行,已知A、B两点的电势分别为φA=12V、φB=6V,则C、D两点的电势可能分别为( )
如图所示,匀强电场中的A、B、C、D点构成一位于纸面内平行四边形,电场强度的方向与纸面平行,已知A、B两点的电势分别为φA=12V、φB=6V,则C、D两点的电势可能分别为( )| A. | 9V、18V | B. | 9V、15V | C. | 0V、6V | D. | 6V、0V |
 在“探究力的平行四边形定则”实验中,某同学用两个弹簧测力计将橡皮筋的端点拉到点O后,作出了这两个拉力F1、F2的图示,再改用一个弹簧测力计将橡皮筋的端点拉到同一点O,此时弹簧测力计的示数为F3=5.0N
在“探究力的平行四边形定则”实验中,某同学用两个弹簧测力计将橡皮筋的端点拉到点O后,作出了这两个拉力F1、F2的图示,再改用一个弹簧测力计将橡皮筋的端点拉到同一点O,此时弹簧测力计的示数为F3=5.0N 如图甲所示的装置,可用于探究恒力做功与速度变化的关系.水平轨道上安装两个光电门,小车上固定有力传感器和挡光板,细线一端与力传感器连接,另一端跨过定滑轮挂上砝码盘.实验时首先保持轨道水平,通过调整砝码盘里砝码的质量让小车做匀速运动以实现平衡摩擦力,再进行后面的操作,并在实验中获得以下测量数据:小车、力传感器和挡光板的总质量M,平衡摩擦力时砝码和砝码盘的总质量m0,挡光板的宽度d,光电门1和2的中心距离s.
如图甲所示的装置,可用于探究恒力做功与速度变化的关系.水平轨道上安装两个光电门,小车上固定有力传感器和挡光板,细线一端与力传感器连接,另一端跨过定滑轮挂上砝码盘.实验时首先保持轨道水平,通过调整砝码盘里砝码的质量让小车做匀速运动以实现平衡摩擦力,再进行后面的操作,并在实验中获得以下测量数据:小车、力传感器和挡光板的总质量M,平衡摩擦力时砝码和砝码盘的总质量m0,挡光板的宽度d,光电门1和2的中心距离s.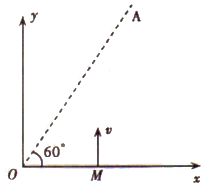 如图所示,在第一象限内有一正三角形区域的有界匀强磁场(未画出),方向垂直纸面向里,磁感应强度大小B=0.5T,一比荷为2×102C/kg的带正电粒子,从M点以v=200m/s的速度垂直x轴方向射入第一象限,粒子射出磁场时,速度方向恰好与OA直线垂直.不计粒子的重力,则:
如图所示,在第一象限内有一正三角形区域的有界匀强磁场(未画出),方向垂直纸面向里,磁感应强度大小B=0.5T,一比荷为2×102C/kg的带正电粒子,从M点以v=200m/s的速度垂直x轴方向射入第一象限,粒子射出磁场时,速度方向恰好与OA直线垂直.不计粒子的重力,则: 小明同学利用如图甲所示的装置来验证机械能守恒定律.A为装有挡光片的钩码,总质量为M,挡光片的挡光宽度为b,轻绳一端与A相连,另一端跨过光滑轻质定滑轮与质量为M的重物B相连.保持A、B静止,测出A的挡光片下端到光电门的距离h,然后将质量为m的小物体放在A上(图中没有画出),A下落过程中经过光电门,光电门可测出挡光片的挡光时间t,算出挡光片经过光电门的平均速度.将其视为A下落h(h>>b)时的速度,重力加速度为g.
小明同学利用如图甲所示的装置来验证机械能守恒定律.A为装有挡光片的钩码,总质量为M,挡光片的挡光宽度为b,轻绳一端与A相连,另一端跨过光滑轻质定滑轮与质量为M的重物B相连.保持A、B静止,测出A的挡光片下端到光电门的距离h,然后将质量为m的小物体放在A上(图中没有画出),A下落过程中经过光电门,光电门可测出挡光片的挡光时间t,算出挡光片经过光电门的平均速度.将其视为A下落h(h>>b)时的速度,重力加速度为g.