题目内容
（12分）如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；一质量为m、电荷量为－q(q>0)的粒子以平行于x轴的速度从y轴上P点处射入电场，已知OP＝L，OQ＝2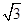
L.不计粒子重力．求：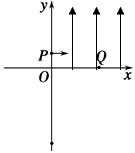
（1）粒子在第一象限中运动的时间．
（2）粒子离开第一象限时速度方向与x轴的夹角．
（1）
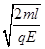（2）θ＝30°.
解析试题分析：带电粒子在电场中做类平抛运动，在y轴负方向上做初速度为零的匀加速运动，设加速度的大小为a，在x轴正方向上做匀速直线运动，设速度为v0，粒子从P点运动到Q点所用的时间为t，则由类平抛运动的规律可得：
L＝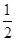
at2 ① (2分)
2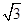L＝v0t ② (2分)
且a＝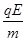
③ (2分)
（1）由①③式得：t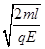＝ . ④ (2分)
（2）设粒子射出第一象限时速度方向与x轴正方向的夹角为θ则
tanθ＝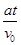
⑤ (2分)
由②③④⑤式，得tanθ＝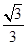
，即θ＝30°. (2分)
考点：考查带点粒子在电场中的偏转
点评：要理解力决定运动的含义，分析运动首先要分析受力，根据本题的受力情况判断运动情况，各分运动具有等时性是求解本题的关键，能够利用运动的合成与分解求解本题也是要考查的能力
练习册系列答案
优加精卷系列答案
相关题目
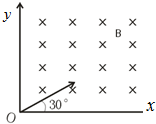（2011?南县模拟）如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对正、负电子分别以相同速度沿与x轴成30°角从原点垂直射入磁场，则正、负电子在磁场中运动时间之比为（ ）
如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对正、负电子分别以相同速度沿与x轴成60°角从原点射入磁场，则正、负电子在磁场中运动时间之比为（ ）
如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对质量和电荷量均相等的正、负离子（不计重力）分别以相同速度沿与x轴成30°角从原点射入磁场，则正、负离子在磁场中（ ）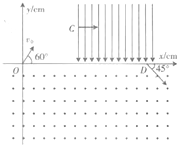
（2013?山西模拟）如图所示，在第一象限0＜x＜6cm的范围内，有一方向垂直于纸面向外、磁感应强度大小为B1=0.8T的圆形匀强磁场区域（图中未画出），在x＞6cm的范围内有沿y轴负方向的匀强电场；第三、四象限内有垂直纸面向外的匀强磁场，磁感应强度B2的大小未知．一个质量m=8.0×10-l2kg、电荷量q=2.0×l0-6C的带正电的粒子，以v0=4.0×l03m/s的速度从坐标原点O沿与x轴正方向成60°角射出，经圆形匀强磁场区域后平行x轴方向到达C（6cm，4cm ）点，之后从C点垂直电场方向射入匀强电场中，并从D点沿与x轴正方向成45°角进入匀强磁场B2中，最后恰好能返回到O点．不计带电粒子的重力，求：
如图所示，在第一象限存在垂直纸面向里大小为B的无限大的匀强磁场，一个质量为m，电量为q带正电的粒子从坐标原点O处以v进人磁场，粒子进入磁场时的速度方向垂直于磁场，且与x轴正方向成30．角，不计重力，则粒子在磁场中运动的时间和半径为（ ）A、t=
| ||
B、t=
| ||
C、R=
| ||
D、R=
|