题目内容
 如图所示,质量为m的小球,由长为l的细线系住,细线的另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=0.5l,过E作水平线EF,在EF上钉铁钉D,若线能承受的最大拉力是9mg,现将小球拉直水平,然后由静止释放,若小球能绕钉子在竖直面内做圆周运动,求钉子位置在水平线上的取值范围.不计线与钉子碰撞时的能量损失.
如图所示,质量为m的小球,由长为l的细线系住,细线的另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=0.5l,过E作水平线EF,在EF上钉铁钉D,若线能承受的最大拉力是9mg,现将小球拉直水平,然后由静止释放,若小球能绕钉子在竖直面内做圆周运动,求钉子位置在水平线上的取值范围.不计线与钉子碰撞时的能量损失.分析:碰钉子后的圆周运动的半径越小越容易满足条件;根据机械能守恒定律和牛顿第二定律分别列式后联立求解出临界半径.
解答:解:这是一个圆周运动与机械能两部分知识综合应用的典型问题.题中涉及两个临界条件:一是线承受的最大拉力不大于9mg;另一个是在圆周运动的最高点的瞬时速度必须不小于
(r 是做圆周运动的半径).设在D点绳刚好承受最大拉力,设DE=x,则:
AD=
悬线碰到钉子后,绕钉做圆周运动的半径为:
r=l-AD=l-
①
当小球落到D点正下方时,绳受到的最大拉力为F,此时小球的速度v,由牛顿第二定律有:
F-mg=
结合 F≤9mg可得
≤8mg ②
由机械能守恒定律得:mg(r+
)=
mv2
即:v2=2g(r+
) ③
由①②③式联立解得:x≤
l
随着x的减小,即钉子左移,绕钉子做圆周运动的半径越来越大.转至最高点的临界速度
也越来越大,但根据机械能守恒定律,半径 r约大,转至最高点的瞬时速度越小,当这个瞬时速度小于临界速度时,小球就不能到达圆的最高点了.
设钉子在G点小球刚能绕钉做圆周运动到达圆的最高点,设EG=x′如图,则

AG=
r′=l-AG=l-
④
在最高点:mg≤
⑤
由机械能守恒定律得:
mg(
-r′)=
mv2 ⑥
由④⑤⑥联立得 x′≥
l
在水平线上EF上钉子的位置范围是:
l≤x′≤
l
答:在水平线上EF上钉子的位置范围是:
l≤x′≤
l.
| gr |
AD=
x2+(
|
悬线碰到钉子后,绕钉做圆周运动的半径为:
r=l-AD=l-
x2+(
|
当小球落到D点正下方时,绳受到的最大拉力为F,此时小球的速度v,由牛顿第二定律有:
F-mg=
| mv2 |
| r |
结合 F≤9mg可得
| mv2 |
| r |
由机械能守恒定律得:mg(r+
| l |
| 2 |
| 1 |
| 2 |
即:v2=2g(r+
| l |
| 2 |
由①②③式联立解得:x≤
| 2 |
| 3 |
随着x的减小,即钉子左移,绕钉子做圆周运动的半径越来越大.转至最高点的临界速度
| gr |
设钉子在G点小球刚能绕钉做圆周运动到达圆的最高点,设EG=x′如图,则

AG=
x2+(
|
r′=l-AG=l-
x2+(
|
在最高点:mg≤
| mv2 |
| r |
由机械能守恒定律得:
mg(
| l |
| 2 |
| 1 |
| 2 |
由④⑤⑥联立得 x′≥
| ||
| 6 |
在水平线上EF上钉子的位置范围是:
| ||
| 6 |
| 2 |
| 3 |
答:在水平线上EF上钉子的位置范围是:
| ||
| 6 |
| 2 |
| 3 |
点评:本题关键找出临界过程,然后根据机械能守恒定律和牛顿第二定律列式后联立求解.

练习册系列答案
相关题目
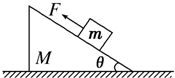 如图所示,质量为M的楔形物块静止在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止,则( )
如图所示,质量为M的楔形物块静止在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止,则( )| A、地面对楔形物块的支持力为(M+m)g | B、地面对楔形物块的摩擦力为零 | C、楔形物块对小物块摩擦力可能为零 | D、小物块一定受到四个力作用 |
 如图所示,质量为M的斜面放置于水平面上,其上有质量为m的小物块,各接触面均无摩擦力,第一次将水平力F1加在M上,第二次将F2加在m上,两次都要求m与M不发生相对滑动,则F1与F2的比为( )
如图所示,质量为M的斜面放置于水平面上,其上有质量为m的小物块,各接触面均无摩擦力,第一次将水平力F1加在M上,第二次将F2加在m上,两次都要求m与M不发生相对滑动,则F1与F2的比为( ) 如图所示,质量为m的小球,距水平面高为2m时,速度的大小为4m/s,方向竖直向下,若球的运动中空气阻力的大小等于重力的0.1倍,与地面相碰的过程中不损失机械能,求:
如图所示,质量为m的小球,距水平面高为2m时,速度的大小为4m/s,方向竖直向下,若球的运动中空气阻力的大小等于重力的0.1倍,与地面相碰的过程中不损失机械能,求: 如图所示,质量为m的小球,从A点由静止开始加速下落,加速度大小为
如图所示,质量为m的小球,从A点由静止开始加速下落,加速度大小为 如图所示,质量为M的人通过定滑轮将质量为m的重物以加速度a上提,重物上升过程,人保持静止.若绳与竖直方向夹角为θ,求:
如图所示,质量为M的人通过定滑轮将质量为m的重物以加速度a上提,重物上升过程,人保持静止.若绳与竖直方向夹角为θ,求: