题目内容
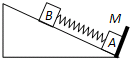 如图,一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上.现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B.已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为EP=
如图,一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上.现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B.已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为EP=| 1 | 2 |
(1)撤掉外力时,物块B的加速度大小;
(2)外力在推动物块B的过程中所做的功;
(3)试判断物块A能否离开挡板M?若A能离开挡板M,求出物块A刚离开挡板M时,物块B的动能;若A不能离开挡板M,求出物块A与挡板M之间的最小作用力.
分析:(1)由弹簧弹性势能的表达式求出弹簧的形变量,然后由牛顿第二定律求出物块B的加速度;
(2)由平衡条件求出物块静止时弹簧的形变量,然后应用动能定理求出推力的功;
(3)求出A恰好离开挡板时系统机械能的增量,根据该能量与系统所具有的机械能的关系判断物块A是否能离开挡板;然后由能量守恒定律、平衡条件求出A与挡板间的作用力.
(2)由平衡条件求出物块静止时弹簧的形变量,然后应用动能定理求出推力的功;
(3)求出A恰好离开挡板时系统机械能的增量,根据该能量与系统所具有的机械能的关系判断物块A是否能离开挡板;然后由能量守恒定律、平衡条件求出A与挡板间的作用力.
解答:解:(1)弹簧具有的势能为EP=5J,
EP=
kx12=
×1000x12=5,
解得,弹簧的压缩量:x1=0.1m,
撤掉外力时,由牛顿第二定律得:
kx1-mBgsinθ=mBa,
解得,物块B的加速度:a=5m/s2;
(2)物块B静止在斜面上时,
由平衡条件得:kx0=mBgsinθ,
解得:x0=0.05m,
外力推动物块B所做的功:
W=EP-
kx02-mBgsinθ(x1-x0),
代入数据解得:W=1.25J;
(3)假设物块A刚好离开挡板M,
弹簧的伸长量x2kx2=mAgsinθ,
解得:x2=0.025m,
此时弹簧的弹性势能和重力势能的增加量之和:
E=
kx22+mBgsinθ(x1+x2)=6.5625J>EP=5J,
故物块A未离开挡板M.
设物块B上滑到速度为零时,弹簧的形变量为x3
若弹簧处于压缩状态:EP=
kx32+mBgsinθ(x1-x3),
x31=0,x32=0.1m(不合理舍掉),
若弹簧处于伸长状态:EP=
kx32+mBgsinθ(x1+x3)
解得:x31=0,x32=-0.1m(不合理舍掉),
综上可得,物块B的速度为零时,弹簧恰好处于原长,
此时物块A对挡板的作用力最小,作用力F=mAgsinθ=25N;
答:(1)撤掉外力时,物块B的加速度为5m/s2;
(2)外力在推动物块B的过程中所做的功为1.25J;
(3)物块A不能离开挡板M;物块A与挡板M之间的最小作用力为25N.
EP=
| 1 |
| 2 |
| 1 |
| 2 |
解得,弹簧的压缩量:x1=0.1m,
撤掉外力时,由牛顿第二定律得:
kx1-mBgsinθ=mBa,
解得,物块B的加速度:a=5m/s2;
(2)物块B静止在斜面上时,
由平衡条件得:kx0=mBgsinθ,
解得:x0=0.05m,
外力推动物块B所做的功:
W=EP-
| 1 |
| 2 |
代入数据解得:W=1.25J;
(3)假设物块A刚好离开挡板M,
弹簧的伸长量x2kx2=mAgsinθ,
解得:x2=0.025m,
此时弹簧的弹性势能和重力势能的增加量之和:
E=
| 1 |
| 2 |
故物块A未离开挡板M.
设物块B上滑到速度为零时,弹簧的形变量为x3
若弹簧处于压缩状态:EP=
| 1 |
| 2 |
x31=0,x32=0.1m(不合理舍掉),
若弹簧处于伸长状态:EP=
| 1 |
| 2 |
解得:x31=0,x32=-0.1m(不合理舍掉),
综上可得,物块B的速度为零时,弹簧恰好处于原长,
此时物块A对挡板的作用力最小,作用力F=mAgsinθ=25N;
答:(1)撤掉外力时,物块B的加速度为5m/s2;
(2)外力在推动物块B的过程中所做的功为1.25J;
(3)物块A不能离开挡板M;物块A与挡板M之间的最小作用力为25N.
点评:弹簧的弹力是变力,分析清楚物理过程,对物体正确受力分析、从能量的角度分析是正确解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,在倾角为θ的斜面上,有一质量为m的通电长导线,电流方向如图,当斜面处于方向垂直于斜面向上的匀强磁场中,磁感强度分别为B1和B2时,斜面与长直导线的静摩擦力均达到最大值,已知B1:B2=3:1,则斜面与长直导线的最大静摩擦力为( )
如图,在倾角为θ的斜面上,有一质量为m的通电长导线,电流方向如图,当斜面处于方向垂直于斜面向上的匀强磁场中,磁感强度分别为B1和B2时,斜面与长直导线的静摩擦力均达到最大值,已知B1:B2=3:1,则斜面与长直导线的最大静摩擦力为( )| A、mgtanθ | ||
| B、mgsinθ | ||
C、
| ||
D、
|
 (2010?杨浦区一模)如图,在倾角θ 为37°的固定光滑斜面上放着一块质量不计的薄板,水平放置的棒OA,A端搁在薄板上,O端装有水平转轴,将薄板沿斜面向上和向下匀速拉动时所需拉力大小之比为2:3,则棒对板的压力大小之比为
(2010?杨浦区一模)如图,在倾角θ 为37°的固定光滑斜面上放着一块质量不计的薄板,水平放置的棒OA,A端搁在薄板上,O端装有水平转轴,将薄板沿斜面向上和向下匀速拉动时所需拉力大小之比为2:3,则棒对板的压力大小之比为 如图,一质量为m的小物块带正电荷Q,开始时让它静止在倾角θ=30°的固定光滑斜面顶端,整个装置放在场强大小为E=mg/Q、方向水平向左的匀强电场中,斜面高为H,释放物块后,物块到达水平地面时的速度大小为(重力加速度为g)( )
如图,一质量为m的小物块带正电荷Q,开始时让它静止在倾角θ=30°的固定光滑斜面顶端,整个装置放在场强大小为E=mg/Q、方向水平向左的匀强电场中,斜面高为H,释放物块后,物块到达水平地面时的速度大小为(重力加速度为g)( ) (2012?杨浦区一模)如图,在倾角θ为37°的固定光滑斜面上放的一块质量不计的薄板,水平放置的棒OA,A端搁在薄板上,O端装有水平转轴,棒和板间的滑动摩擦系数为
(2012?杨浦区一模)如图,在倾角θ为37°的固定光滑斜面上放的一块质量不计的薄板,水平放置的棒OA,A端搁在薄板上,O端装有水平转轴,棒和板间的滑动摩擦系数为